Differentiating by Assessment

Bless me Father for I have sinned. It’s been four and a half years since my last curriculum article.

My entire teaching career has been spent navigating a student ability gap that got noticeably wider sometime before the pandemic. The strongest kids are getting better, the weaker ones spent middle school not learning a thing because they’d pass anyway. (Thank you, Common Core.)

I am constitutionally incapable of giving an F to kids who show  up and work. Call it a failing if you must. So yes, the gap grew, but I adjusted and got back to moving the unengaged kids forward, building the confidence of the kids willing to play along, and pushing the top kids as far possible, given the ability ranges.

But tests were increasingly a problem. My long-standing approach was to allow all students extra time to finish tests or ask questions. But this was premised on a much smaller gap and by this time the gap is a  canyon. Add to that the fact that cheating is just an enormous issue post-pandemic, so giving kids access to the tests after school and at lunch increases the chance of them getting a camera on the questions, posting it on Discord, using photomath, memorizing the question to ask a classmate, whatever. Once upon a time, kids were just grateful to have the chance for extra time, but lo, those were the days of yore. So I want more kids finishing all or most of the test within a single class, and if they need extra time I want it wrapped up quickly.

To understand the nature of my dilemma: If I build a quiz that my weakest kids (10-20% of the class) can get a high F, D, or C after the entire class period and an hour of additional supported work, the top kids (30-40% of the class) will  finish it in 10 minutes. I’ve given quizzes that the top kids are handing in before I’ve finished handing them out.

That’s just straightforward quizzes. How do you build a cumulative unit test that challenges your best kids that your weakest kids won’t flunk by giving up  20 points? Or takes them eight hours to work through and then flunk with 40 points? How do you make something manageable for your strugglers that isn’t a five minute exercise for your strongest students? 

The idea hit me in November when I was building the unit two test. I’d pulled up last year’s version. It was a good test, but the strongest kids had finished it in 40 minutes, and the weakest students from that class were far better than my 30 weakest students (out of 150) from this year. So I’d be giving a test that the best kids would blitz through, the middle kids would struggle with, and the weakest kids would give up and start randomly bubbling.

As mentioned, I’ve got just the one prep. So instead of this two or three weak students, 10-12 strong students, it’s 40 weak students, 60 strong ones, and 40 midrange.

Never mind the aggravation, it’s just crap, pedagogically speaking. My weaker students need math they can do, build up their confidence. My strong kids need…doubt. Challenge. Something more than the straightforward questions that strugglers need.

Suddenly a familiar thought snuck in: I could create two tests. Not two different versions of the same test. Two tests of entirely different questions on the same topics, one much less challenging than the other.

Familiar because I’ve wanted to do this …well, since before the pandemic, at least five years ago, when I first accepted that the gap wasn’t getting any better. But every other time I dismissed the notion. I usually teach from five to seven different classes a year, so that would be 10 to 14 tests, some of which would only be taken by five or six students. Not worth it.

But hey. I’ve got just the one prep.

Maybe I could make a little lemonade.

Requirements:

1. The tests had to have the same number of questions, the same answer choices, tests the same topics. I build my own scan sheets and I wanted to be able to make each test a different version on the same scantron.
2. Questions had to be on the same topic. I organize my tests by section, with each section having from 4 to 6 questions. The situations presented in each test had to be on the same general topic, and the questions asked had to explore the same knowledge base.
3. My weak students couldn’t get As or Bs on their tests. I couldn’t say “an A on this test is really a C”. The easy test had to be hard enough for my weak students to get a C or B- at best. I wouldn’t have even considered taking this on without confidence in my test development skills, but admitting failure had to be on the table
4. I had to be accurately categorizing students. The “easy test” scores had to be overwhelmingly C or lower with only a few outliers doing well, and no As. The “hard test” could have more variance, as I already suspected some degree of cheating at the high end of my class, but well north of half the students needed to come out of the first test with an 85% of higher. If I met this objective, then I’d decide what to do with the kids who scored too high or too low. But if I had too many students flunking the hard test or acing the easy test, then my whole theory of action was flawed and I had to give up on the idea.

So I made two tests–well, technically, two tests with three versions. Two versions of a challenging test, one I thought would really push the median B student in my class.  One version of a test that I thought would be manageable but tough for the strugglers.

About a hundred students got the hard tests; forty something got the easy test.

Results of the first scan:

• Half of the “hard test” students got an A. Another 10% got a high B, which I counted as an A (this was a tough test). Another 10% got between 75 and 85%, indicating they knew what they were doing and just had a few fixes. The rest tanked badly, scores of 30-60%. More false positives than I expected, but enlightening. These students clearly knew more than my strugglers but there was a clear ability line separating them from the top students. I had a bigger middle than I knew.
• All but two of the weak kids got above 50% on the easy test (two didn’t finish), but only three got 80%, and about 10 got above 70.

I was accurately categorizing students. Well enough at least to continue. And I have, since then, on both tests and quizzes.

The “middle” students needed a mama bear test, and I built a new one that did the job. From that point on I always created three tests, which allows me more flexibility in moving students around. I only build two quizzes (again, I’m talking about difficulty levels; I still build multiple versions of each quiz to cut down on cheating). About 60 kids take the hard test, 40 taking the middle and 40 taking the easy version.

I’m extremely pleased with the results. First, my top kids love the harder tests. A number of students who just thought they were top kids got a dose of humility and started paying more attention. I’ve made math harder for them in, I think, a positive way. They can’t complain that I’m being unreasonable when a fourth of the students are acing the harder tests.

But the real impact has been on my strugglers, who range in motivation from absolutely none to never stops plugging away. They work harder on the tests and quizzes instead of just giving up. They work more in class, finally seeing a link between their effort and achievement. While they all still have difficulty on unit tests and integrating their knowledge, their quiz scores have seen considerable boosts. I’ve actually been able to make the “easy” quizzes more difficult and still see high passage rates.

Regular readers will note a recurring theme of mine: My weaker students are learning more not because I raised standards, but because I lowered them.

Allow me to quote the degenerate wise man, Joe Gideon, once more: Listen. I can’t make you a great dancer. I don’t even know if I can make you a good dancer. But, if you keep trying and don’t quit, I know I can make you a better dancer.

Rigor and high expectations are, forgive me, not the way to make kids better students.

Anyway. It’s working. My weak kids are doing better and my top kids are getting stretched. Score a single lonely point for giving me just one prep.

********************************************************************************

Some notes:

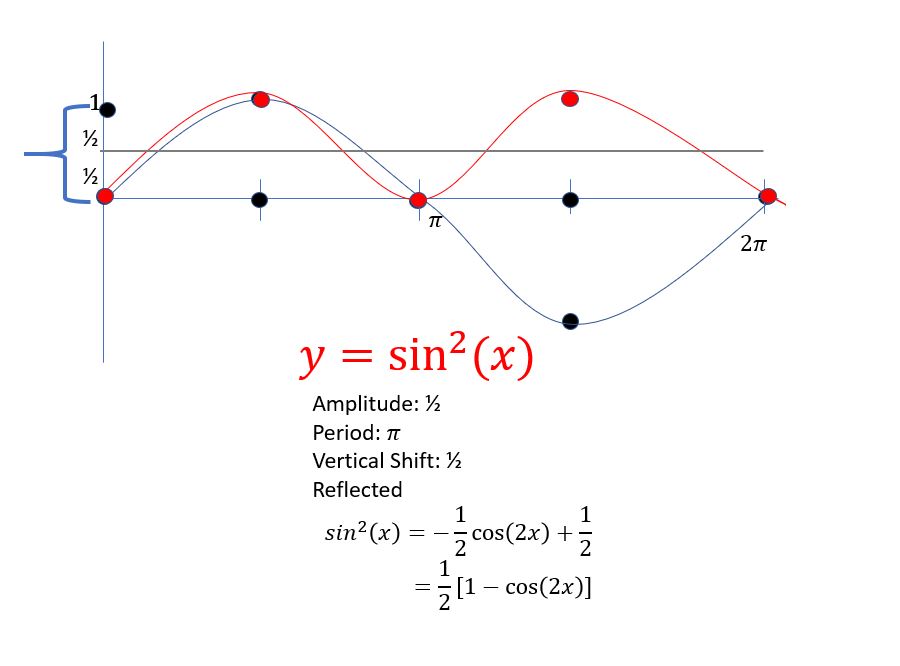
Back in 2015, I wrote a lot about my “multiple answer math tests“, as I called them–inaccurately. I still use them, updated them to a scan sheet. Given how essential and permanent these tests are in my work,it’s odd I haven’t written about the format since. To understand this post, you may want to read about the test structure, which is somewhat unusual, I think. I’ve changed the format somewhat since then, with less T/F, but the organization of multiple broad topics with many questions per topic is the same.

While students get the same points for questions, I weight some free response questions with more points on the harder tests. Not always, but sometimes the questions are in entirely different orbits of difficulty. Still, I keep an eye out for students who are getting all the questions right on the easier tests, as it’s a sign they need to move up.

Students have moved up and down. Three or four strong students were coasting off of the easier tests and like their phones way too much. Some figured this out and got serious, others didn’t. Some students have moved permanently from the low test to the mid-range test.

Ever since I found my test on Discord last year I’ve quit returning tests, which makes all this much easier. The top students have realized there are different tests beyond just versions, but after a few questions early on they quit mentioning it. They all seem to like it.

I almost gave up on this post twice because I couldn’t figure out how to display images of the different difficulty levels on the page. Here are some examples:

• Segment Addition with Algebra
• Area and Perimeter
• Angle Pairs and Algebra
• Triangle Centers and Coordinate Geometry

Larry Cuban: Understanding the Stability of American Schools

(Disclosure: Larry Cuban is a friend, but my opinions on his value originated long before I met him.)

Over 20 years ago, Franklin Foer extolled conventional wisdom (CW) and its avatar,  David Gergen, arguing that Gergen’s relentlessly conventional wisdom was based on his deep expertise, which led him to unflashy but unerringly correct conclusions.

Until starting this piece I’d forgotten the author, the date, and the publication. My memory said the CW exemplar was David Broder, which made finding the article nearly impossible. 

What stayed with me was the plainly correct observation that flashy, controversial and ultimately flawed “takes” are given more public attention than accurate analyses yielding  prosaic outcomes reflecting the status quo.

Larry Cuban is a writer, historian, teacher, and educator who built a career pointing out that no Big Idea, whether it be driven by technology, “science”, money, standards, leadership, or organizational mandates, is likely to change the implacable stability of American education. And he gets it right. A lot.

Just as David Gergen has been banking on his “boring” takes for decades, Larry has been successful in education policy despite his avoidance of bold, controversial policies and predictions. Popular Stanford professor and co-author of a  famous text on education reform, he has made Rick Hess’s list of prominent edu-scholars every year since it came out in 2012.  

In ed school, we were assigned a chapter Larry wrote on problems versus dilemmas, a frequent topic on his long-running blog.  I initially dismissed his observations because I confused his insights with the teachers’ values. One wanted to support her students by advocating rent control but she might lose her job, for example. But we reread the piece after seven months of student teaching and I realized that the dichotomy was essential regardless of the examples. Today it’s hard to avoid the reality that most if not all education policy debates are dilemmas  wrongly pegged as  problems.* Accept this reality and it’s a short step to understanding that little will change.

Larry recently wrote a memoir, one I strongly recommend, although my  book reviews usually run to multi-part articles filled with examples and arguments on the author’s many misconceptions. (No David Gergen, I.) 

Larry structures his life story around America’s three eras of education reform, which correspond with his own education and career. His childhood took place in the fading days of the  Progressive Era, characterized by rapid secondary school expansion and increased focus on education administration and methods. His immigrant parents worked in New York City until they could buy n their own grocery store in Passaic, New Jersey, where Larry was born. Forced into bankruptcy by  anti-Semitic boycotts of all Jewish-owned stores, they relocated to Pittsburgh to be with family. An average student who preferred history and science, Larry’s memories of school are quite fuzzy, although he clearly recalls lessons of both traditional  and progressive approaches. More vivid memories involve sports and friends, a core group of whom he has stayed in touch with for seventy years.

The next section, my favorite, focuses on the Civil Rights era in education reform, from the late 50s to the early 70s. Larry majored in biology and history education. His first job was as a science teacher, but his strong desire to teach US history led to employment in a 99% “Negro” school in Cleveland, Ohio, a job that set the trajectory of his career. Lecturing to bored students five classes a day enervated and depressed him, so he started typing up primary sources of black history in an attempt to create classes more like his graduate seminars.  In a few years he became a notable teacher expert at engaging black students, qualifying for a year seminar in Yale. 

From there, Larry’s career becomes a roadmap of major 60s initiatives. He was invited to Washington, DC to head the Cardozo Project in Urban Teaching initiative, training returning Peace Corps volunteers to teach and build curriculum, originally a one-year project that his successful leadership converted into continued extensions. Ultimately the model was adopted first as DC’s Urban Teacher Corp and then as a model for the National Teacher Corps. He tried federal employment as a director of race and education at the Commission on Civil Rights, but he wasn’t a happy administrator. The horror of Martin Luther King’s assassination created racial tensions in the diverse office staff, so he left and enjoyed a few months of unemployment as a stay at home dad. He then went back to the DC district and worked in staff development until office politics drove him out. 

 Larry’s blazing early success in teaching drove his initial belief that curriculum and engagement could close the achievement gap and drive societal change. Witnessing the politics and obstruction of his ideas at the federal and state level changed his opinion: the  “best unit of reform” was a leadership position. But the ability to influence and reform as an administrator would require either  experience or more education.  Although Larry had kept teaching all through this period, covering one or two periods of history a day at a local school, he hadn’t stayed anywhere long enough to start an administrative career–and doing so would take a number of years. So off he went to Stanford to get a doctorate as a shorter path to a leadership position.  

The Civil Rights era of Larry’s career offers wonderful insights into teaching and education politics of an earlier era**. Larry’s brief recollections of ed school as well as his efforts to teach in a manner consistent with his training also sounds really familiar. I’m reminded again that many aspects of the education debate have a much longer timeline, one that most ed schol  critics ignore.

In person and writing, Larry is calm and laid back, making it easy to miss the ambition drove many of his career decisions (although his deep love for wife and daughters as well as his long-running friendships come through).  His decision to pursue a doctorate for professional advancement led to his superintendency at Arlington Schools superintendent, which begins the book’s third section on the Standards Based Reform Movement, from the 70s until today. He was hired by a politically liberal school board (including Ann Broder, David’s wife–how plate o’ shrimp it would have been had Broder been the CW maven!). The internet still yields a  number of stories that support Larry’s recollections, including an epic revenge reversal that’s hard not to enjoy as sheer story-telling despite the outcome, which ultimately led to his ouster when a more conservative electorate flipped the school board.  

Larry’s account details the national shift from focusing solely on black  achievement to managing the needs and challenges of an economically, racially, and academically diverse student body. While he never neglected the practical aspects of superintendency–keeping the lights on, parental communication, board relationships, learning and test scores–both his memoir and contemporaneous reporting reveal his emphasis on instruction and instructors.  He visited classrooms weekly for all seven years of his superintendency and had a standing offer to join teachers for lunch and discussion. He offered workshops on observations and  inquiry-based questioning skills. He’d sub from time to time. 

Biiennial surveys during his seven year reign showed increasing parental satisfaction. Test scores in elementary school improved, while secondary school scores stagnated. (Twas ever thus.) Significantly, Larry’s successor lasted only one term and was fired when the school board flipped back to the left. By then, Larry had returned to Stanford where he’s been ever since, publishing over 20 books since retiring in 2001.

Larry’s memoir does much to explain his scholarly focus and philosophy. His sketchy memories of his own school experiences renewed his perspective on the relative importance of education: Or, as he says in the memoir, “Life educates.”

His success in improving engagement led to his conviction that meaningful curriculum and trained teachers would lead the way to greater learning. When he found constraints, he sought to broaden that “best unit of reform” –first trying policy, then in district management. Ultimately, Larry realized that his initial belief that “better schools could make a better society” had the “causal direction wrong: societal changes alter schools far more than schools remake society”.

His scholarship continually reflects this theme. Larry’s seminal work Tinkering Towards Utopia, written with his friend and colleague David Tyack, informed and warned passionate choice and accountability advocates about the cycles of earlier reform eras.  In 1995, the modern education reform movement was gathering steam, the federal government was enabling charters to “compete” with public schools so they could “end the achievement gap”. National curriculum reform was being attempted in every academic subject. Triumphalism was the tone of the day. Meanwhile Cuban and Tyack were pointing out how often this had been tried–and failed–before. ESA and voucher advocates would be wise to take note.

In As Good As It Gets, he explored a decade of Austin’s school reform under the same superintendent.  Larry observes that relatively little changed in the classroom and to the extent it did no link to management policy implementation could be ascertained. The title is double edged, praise with a shrug: hey, you want reform? This is about as good as it gets. 

As reform movements sought to use technology as the new tool to transform the classroom,  Larry reported the actual impact. Oversold and Underused, captures his thesis: computers in the classroom haven’t changed much about instruction or curriculum.

Larry’s books continually remind us of the strength of the conventional education models: for all we argue, nothing in education changes much. He views American schools’ implacable resistance to change with cheerful equanimity.  It is what it is, something to be accepted and even cherished, despite the inequities. I suspect Larry wouldn’t object much to Arnold Kling’s Null Hypothesis of Education Intervention. 

Although Larry supports charter schools, his message often runs contrary to reform rhetoric. Once he participated as a panelist in a 2015 AEI round table on classroom changes wrought by “billionaire philanthropy” for education reform. His presentation included this deeply Cubanesque slide predicting that most reforms will disappear, and the ones that don’t will actually strengthen the conventional form of public education. 

Howard Fuller, up next, responded with doleful humor: “It’s always difficult to read Larry’s stuff because then you want to go back in your house. It’s like ‘why did I leave my house today?’ you know, given how little leaving my house means to anybody…but after having fought through that, I decided to get on the plane anyway.” 

Acceptance doesn’t mean indifference. As I first observed over a decade ago,  Larry is one of just two well-known education policy experts who has significant experience as a teacher, a job he dearly loved and that clearly influences his research and findings. Above all, he seeks to inform his readers on the act of teaching and its disconnection from the far more visible policy debates. He loves to visit working classrooms. His books carry multiple, careful and detailed lesson observations, either those he witnesses himself or those he culled from archives and news reports. Anyone who simply wants to know what happens when teachers shut the doors in  America’s classrooms would be well-advised to read his work.

In years, decades, and even centuries to come, when historians are snorfling loudly at publishers who promoted nonsense like Richard Reeves’  treatise arguing we should keep boys back a year, they will still be reading Larry’s books for insight into America’s teaching force throughout history.

*****************************************************

*Examples in my own work: Algebra 2, the Gateway Course, The Day Of Three Miracles, The Push for Black Teachers, Minneapolis Style. Another ed school author who made much more sense on the second reread was Grant Wiggins. 

**Teaching History Then and Now has more such stories for those interested.

Ten Most Read, Ten You Should Read

Eight years ago, on the second anniversary of my blog, I asked, “Am I a hedgehog or a fox?”  Hilarious, that I could ever be so deluded. I understand why my brain thinks itself a hedgehog, but it will just have to cope with reality.

I am a fox. Even at my lowly level of the word, this is a list only a fox could produce.

Ten Most Read Articles:

1. More than Gotcha: Kamala’s Busing Blunder— June 28, 2019
   The only item past its sell date. Most of my work maintains its relevance. But this article, outdated though it is, has a good number of my strengths on display. First, unlike the entire media class, I know how to search for and use relevant history. No one listening should have thought anything other than “that’s bullshit” when she claimed to have been on the frontlines of segregation in Berkeley, CA. But no journalist bothered to do the research. Next, I understood as no one else seemed to that she was essentially coming out in favor of busing.  At a time when most of the media (and all of Twitter) was wowed, I  pointed out she’d almost certainly have to walk that comment back. The other strength: sometimes I really hate people while many other folks are like, man, why is Ed hating on her and then later they go oh, I get it.
   ignore me, lazy way to space
2. Asian Immigrants and What No One Mentions Aloud–October 8, 2013
   I’ve kind of cornered the market in Asian immigrant criticism–not of the people, but of the culture, which I think is very damaging to American education. I wouldn’t make such a big deal out of it if everyone else weren’t determined not to notice. This was the first time I wrote about it.
   ignore me, lazy way to space
   
3. Functions vs. Equations: f(x) is y and more — May 24, 2015
   A math curriculum piece in third place? Blew me away. But as I mentioned, curriculum searches are specific and get through Google’s recency bias, so they’re the one article category that still gets fed via search engines. I keep meaning to revisit this article because it had a very bimodal reaction. Mathy readers who didn’t teach were aggravated and confused by the article and told me I didn’t understand the math. On the other hand, a number of professors on Twitter understood my point  instantly and were very appreciative (and some later commented as well). I think the mathy folks thought I was confusing a system with a function, whereas the professors understood I was using an example of multiple equations that wasn’t a system to show students a difference they hadn’t seen before.
   ignore me, lazy way to space
4. Homework and grades–February 6, 2012
   I have relatively few strong views about what teachers should do. Homework is the exception. Homework is insane. Grades are fraud.
   ignore me, lazy way to space
5. Algebra and the Pointlessness of The Whole Damn Thing— August 19, 2012
   My first really huge piece, and one I’m still quite fond of. It’s getting harder to find data easily; more states are hiding racial and economic distinctions. But if you look at current data, you’ll see the same pattern: poor whites do about as well as non-poor blacks and Hispanics. Been like that for decades.
   ignore me, lazy way to space
6. Philip Dick, Preschool and Schrödinger’s Cat — April 5, 2013
   Canonical Ed on IQ.
   ignore me, lazy way to space
7. Binomial Multiplication and Factoring Trinomials with The Rectangle— September 14, 2012
   Another curriculum piece. I took a long time to make sure the figures and explanations were thorough. I hope other teachers get good use from it. Still the best way to teach factoring, even if your kids don’t use it.
   ignore me, lazy way to space
8. The myth of “they weren’t ever taught….”— July 1, 2012
   This is one of my favorite pieces. It’s all true, still. Every word. And new teachers have to come to grips with it every year.
   ignore me, lazy way to space
9. The SAT is Corrupt. No One Wants to Know.–December 31, 2014
   I am adamantly opposed to grades-based college admissions. But the College Board is corrupt. The international SAT is corrupt. And they’ve changed it in ways to make it far less useful, all in the hopes of ending the score gap, which was never going to happen.
   ignore me, lazy way to space
10. The Gap in the GRE–January 28, 2012
    Another of my favorite pieces that asks a very good question: why are genuine high achievers in verbal tests so less frequent than in math tests? Note that in the intervening years, the College Board and the ETS have eliminated all the verbal difficulty in the SAT and the GRE.

So there’s my ten most popular.

Then I just looked over all my articles and looked for favorites that also captured my zeitgeist (can people have zeitgeist?). I was particularly looking for self-contained articles–a lot of time I go down one rabbit hole and then get to the main point. (Yes, I’m thinking of those for my rewrite plans.) I also wanted a good sample.

1. Teacher Quality Pseudofacts, Part II–January 15, 2012
   This is a top 20 all-time post and was a steady performer for years. I almost didn’t include it; today it seems kind of old hat. But in fairness, that’s like saying 1933’s 42nd Street is cliché because it uses all the old tropes about movie musicals. It didn’t use them. It invented them. When I wrote this article, it was common wisdom that teachers were low-skilled, low-quality, and not very bright. Only the terminally uninformed, the amateurs and the hacks,  have made that claim in four or five years.  I like to think Pseudofacts has had something to do with that change,  because of the very easily found data I brought to light.
   ignore me, lazy way to space
2. The false god of elementary school test scores–July 30, 2012
   Another one I almost didn’t include because it definitely has the rabbit hole problem about Rocket Ship at the beginning. However, like Pseudofacts, it’s an early example of my actually looking at readily available information and pointing out the obvious. Plus, great title.
   ignore me, lazy way to space
3. The Fallacy at the Heart of All Reform–September 7, 2012
   I wrote a history of modern education reform throughout much of 2020-21. This was a history of earlier policy. But the definition of fallacy I include here holds for the entire era.
   ignore me, lazy way to space
4. The Day of Three Miracles— April 28, 2015
   I don’t often talk about colleagues, mainly because for years my relationship with them was….fraught. Not bad, just…there. But this is not only a colleague story, it captures a conundrum that few people in education policy seem to understand. Access or rigor. Not both.
   ignore me, lazy way to space
5. Citizens, Not Americans— June 16, 2016
   I love this piece. By the way, Dwayne is married, has a kid, and is in the military. Abdul went to a top tier school and majored in pharmacy, and when he told me I want “Gack!” and he said “yeah, I know. Stupid move.” and now he’s getting an MA in nurse practitioner, or whatever it’s called. Haven’t heard from Chuy. Wing and Benny still teach. One of them is now department chair, and I had a lot to do with it.
   ignore me, lazy way to space
6. “Get Out” a scathing satire? Get Out.–January 22, 2018
   I love movies, and I know as much about American diversity as anyone in the country, and I think this is a terrific review that isn’t at all what you’ll expect.
   ignore me, lazy way to space
7. Algebra 2, the Gateway Course–January 28, 2018
   Another story about colleagues, students, and really stupid education policy.
   ignore me, lazy way to space
8. Making Rob Long Uncomfortable–December 24, 2018
   Silly title, but you can listen to the podcast and see what I mean. It’s well-written, and captures a certain mindset among the centrist conservative punditocracy. As I wrote: “You could practically hear Rob’s toenails shrieking against the tiles as he braked to a stop.  This was not the conversation he’d signed up for. He was there to lightly mock feminists and social justice nuts, not crack witty, on-the-nose jokes with Heather about the racial skills deficit.”
   ignore me, lazy way to space
   
9. The Students of My Christmas Present— December 25, 2018
   I don’t often get sentimental. And I’ve put up Christmas trees most years since.
   ignore me, lazy way to space
10. Idiosyncratic Explanations for Teacher Shortages–May 31, 2019
    Here I raise an issue that seems quite obvious, but isn’t. We have thousands, if not millions, of unemployed PhDs who will never get a tenured job and work as poorly paid adjuncts. Why don’t they become teachers? After all, everyone says we need smarter teachers, right? There’s a cognitive dissonance revealed in the fact that everyone understands that a poorly paid PhD is acting rationally in refusing to take a better-paid, more secure job with great benefits.
    ignore me, lazy way to space
    I thought I was done, but 2017 spoke up, really pissed off. Why nothing? I tried reassurance. It was nothing personal. I wrote some good shit that year. Besides, 2020 and 2021 aren’t represented either. But it would not be assuaged and as my mother isn’t doing well, and this is a not only an ode to American schools but also a lovely story about my mom, an extra…
    ignore me, lazy way to space
11. What the Public Means by “Public Education”–March 19, 2017
    When education reformers wonder why everything went wrong, they should think about the thoughts expressed here.

Thanks for reading.

Coins Dropping, Lights Dawning, and Other Impossibilities

So I was just snotty to Aaron Sibarium last night and now I feel mean. 

I should be gracious to the guy who took on a topic I’ve been howling about for months. My point: for all the hysteria about “leftists taking over public schools” as the ads on NRO podcasts bleat, parents have far more control over public schools than they do private schools and charters. The real CRT insanity is taking hold at the most elite private schools and is a much bigger problem at charter schools than it is at public schools. (When I was in ed school over a decade ago, one of my adjunct professors was leaving to start an all black charter school that was devoted to critical race theory, although she didn’t call it that).

Not that Sibarium mention charter schools at all, or even correctly identifies the problem with private school wokeness. I mean, he’s completely wrong in arguing that an ideological cartel of gatekeepers is keeping Dalton and other elite private schools from abandoning DIE dogma. That’s hilariously nuts. But he gets closer to the point here:

The challenge for both proposals is the college admissions process. In interviews with the Free Beacon, multiple parents expressed concern that elite universities would not look kindly on schools outside the accreditation establishment, which could handicap their kids’ odds of getting in. “The better the school, the more woke it is,” one mother said—”because all the best colleges are woke.” If Dalton is held hostage by the accreditors, parents are held hostage by the meritocracy.

The last sentence is where he goes wrong: like there are Dalton administrators blinking in code: “Send help. End cartel.” But the rest of it correctly identifies the real problem, which is that parents are more interested in access than education.

But the real reason I approve of Aaron’s article is here:

All this poses a problem for market-based education reform: For many parents, there is no market. Far from offering more choice than public schools, private schools may offer even less.

Hahahaha. Yeah,  no shit, Aaron! Well done!  Seriously–he’s maybe 25 years old and says the unsayable. 

And I was mean to him anyway, because first, he’s wrong about the cartel nonsense, but most importantly because of a tweet comment:

If you want school choice to actually offer choice, you’ve got to go after the woke bureaucracy that stifles market competition.

The sound you hear is the point whizzing over Aaron’s head.

The less important wrongness is, again, that Aaron gets the cause completely backwards. As he already pointed out, parents choose these schools for access, not education. The “woke bureaucracy” isn’t the reason there are no excellent conservative private schools that are a pipeline to the Ivies. Elite colleges manage that gatekeeping all by themselves. The “woke bureaucracies” aren’t gatekeepers. While I haven’t looked into it, my first guess is that the various organizations and consulting groups are full-employment mandates for well-connected spouses, much in the way we pretend that Michelle Obama had an important job at a hospital when in fact she got the job when her husband got important. They aren’t powerful. The jobs aren’t powerful. The jobs are mostly wife sinecures. That’s my guess, anyway.

But the really important issue here is way meta, and it’s in the opener: “If you want school choice to actually offer choice”…

Think about it.

Thirty years. THIRTY YEARS conservatives have been pushing school choice. THIRTY YEARS they’ve been howling about the evil public school cartels. THIRTY YEARS their only solution to any education problem was the wholesale destruction of public schools.

Result? Almost every initiative they won during a 16-year reign of bipartisan state and federal legislation was ripped out and declared a total failure by the voters and general public. If education reform organizations were held to the same criteria they demand for teachers, Rick Hess, Michael Petrilli, Nat Malkus, Matt Chingos, and a host of other think tankers would be on unemployment.

I do believe it’s finally sunk in that the institutions, private schools AND charters, that conservatives have been pushing as the right and proper solution to “government schools” are unrelentingly dedicated to the wholesale destruction of everything conservatives hold dear: free speech, merit, academic achieve ment, high standards. Everything that conservatives held the evil teachers’ unions responsible for is now more present, more powerful, and more destructive than before.

But here’s Aaron, offering a fix: “If you want school choice….”

Dude. Some humility.

If nothing else, the smoking, hulking wreck of conservative dreams should give them all pause. Perhaps–I’m gonna just throw this idea out there–perhaps school choice isn’t going to do a damn thing to achieve your goals. In fact, perhaps school choice is an actively wrong answer. Perhaps, given that the organizations you dreamed of are dedicated to your obliteration, you should stop trying to obliterate public schools.

Just a thought.

But in any case, stop offering fixes, Aaron. and everyone else. It’s time to acknowledge that school choice has failed in critical ways to advance conservative or even Republican agendas.  Be a little less flip with solutions.

As a Republican, if not a conservative, who knows public schools are a lot better and far more responsive to communities than the choice shrines, I have no definitive answers. But I have some thoughts. 

School choice gives power to schools, not parents.

The right to attend a local public school is near absolute. The right to attend charters, magnets, and private schools is non-existent. The school choice movement works on the fringes, appealing to the parents who don’t have the money to choose their kids’ peers. It’s not a serious universal solution. Parents know this very well. Schools of choice can always reject the kids and teachers they don’t want, which allows them to enforce ideological demands.

Public schools respond to community demands. Private schools don’t have to.

Naturally, conservatives get this entirely backwards. Never has this been more obvious than in the recent pandemic year. Yes, private schools were more likely to offer in-person instruction. Duh. Why pay for zoom school when you can get it for free? But charters were as likely to be in hybrid or remote as publics were, and for the same reason: parent demand. It was parents, coupled with idiotic state-wide restriction, that kept schools in remote. Every single take blaming teachers unions is goofy. Don’t believe me? Maybe Andrew Smarick, conservative and choice advocate in good standing, will convince you:

The comfort of citizens and parents in any particular geography—not missives from the CDC, studies from universities, or prodding from politicians—is proving to be the key factor in returning to normal. Indeed, though school systems have gotten lousy press for months on end, there might come a time when we see the behavior of American K-12 education during the COVID era as typifying decentralization and democracy in action.

And remember this: anywhere schools opened, teachers went back to work.

Right now, while private school parents are chafing at the woke theology their kids are subjected to, public school parents are voting out school boards and demanding their legislators ban CRT instruction. Public schools are a hell of a lot more democratic than they’re given credit for.

While I’m supportive of CRT laws, remember they’ll only go so far precisely because of local control. Go into any inner city school and odds are the history teachers are using CRT lessons to keep their kids engaged. Try the same thing in the suburbs of Tennessee or Florida and the teacher will be summarily canned.

1 in 3 teachers are Republicans

Do you know who they are? Have you bothered to talk to them? I don’t mean the Fordham Institute-sponsored puppets who mouth the choice dogma that gets them published, but rather the every day teachers who vote for Republicans but don’t think public schools are irretrievably broken. Like me, except probably in red states where it’s not instant suicide to come forward.

Might want to find out who they are, what they think, and how you could support them and maybe make more of them. Hint: best not talk about how useless teachers are, and “we don’t hate teachers, just teachers unions” line won’t reassure them.

Focus your energy on college, not high school

I have been writing about the wholesale destruction of college diplomas for years. It’s a huge problem. Conservatives correctly complain that college isn’t for everyone, but no one is pushing Congress to do anything about it. 

Weakening private colleges and strengthening state colleges is key to addressing the gatekeeping issues that Aaron correctly observes in his article. 

The best solution: Mandate a minimum demonstrated ability level for college loans (Congress) or state universities (state legislatures): Nothing too high. Something like a 550 SAT section minimum, or a composite 25 ACT. Be flexible–we could use more competition in the test market. This suggestion has HUGE disparate impact problems and will be the subject of endless lawsuits, so get started on it now.

I realize all of these suggestions, as well as a host of others I left off because of time and focus factors, are anathema to the people in a position to work on enacting them.  Because Sibarium’s article makes it clear that no one is rethinking things. The coin ain’t dropping. The light ain’t dawning. Textbook definition of insanity runs all through his piece.

But I’m a teacher in a Title I school, which makes me an expert in teaching people who take a long time to learn.

*********************************************************************************

This the first actual Ed_Realist article I’ve been able to write in months, so I’m not going in depth on these and didn’t have time to support with links to things I consider obvious. Spending time trying to craft this would add it to the large pile of unfinished pieces in my draft folder. So I just decided to put these thoughts out there rather than endlessly mull the best way to write this. 

 

Five Things I Learned Remote Teaching Summer School

Attendance is a lot better when grades are involved.

Back in March, a younger, more innocent me argued in favor of excusing students who didn’t show up for high school classes after the shutdown. They didn’t sign up for online school. School is an obligation that society shunts on kids, and it has certain boundaries and (yes, really) choices. So if some students didn’t wake up on time and gave up, or decided that a grocery store hourly wage was a better use of their day, I was all in favor of holding them harmless from that decision. Their choice. In my view, they should not be penalized for that choice. No “F”. No delayed graduation. Take the class off their transcript, reduce the credits for graduation.

Silly me, not to anticipate that some districts and unions would band together and decide that if some kids couldn’t perform, then everyone must pass. Some schools froze grades at point of shutdown, others mandated the even more disastrous credit/ no credit for everyone. In both cases, students could skip school entirely and move on to the next class in the sequence so long as they were passing in March. In the second case, students could work hard and learn or never show up and get the same grade. In my particular school’s case, kids who didn’t show were literally missing an entire semester. Didn’t matter. Even in math. They passed with the same grade as the students who attended zoom sessions, asked questions, learned. And don’t try to feed me any shit about how the hardworking kids earned a moral victory, because without college admissions tests there’s no difference between a kid who didn’t learn anything and a kid who did, if the teachers were forced to give them both a pass.

I wrote half an article about this before I realized I was ranting. Peace.

Anyway. In summer school and, I dearly hope, this fall, teachers can give out grades. I had good attendance all summer.

So from now on when you read those stories about absentee students, remember to email the reporter and ask if the students who didn’t show were guaranteed passing grades and knew it.

Brand new students you’ve never met before? Not a problem. 

One thing everyone seemed certain of last spring was that remote learning only worked because teachers had existing relationships with their students. I worried about that, too. Happy news: that turned out to not be a thing.

I don’t do team building exercises, don’t spend lots of time getting to know my kids. None of this made a difference. I had roughly 25 students in two classes, but all but about five of them were taking both sessions (algebra semester 1 and 2). So about 30-32 students total.  None of them were from my school. I didn’t like remote teaching, but I still routinely received the two plaudits that comprise my success metric: probably 25% of my students said “I like the way you teach so much better; I’m really getting this.” and by direct count eight parents sent me a note saying their kids had mentioned how much they like my teaching. I say this not to brag, but because, well,  I’m a pretty darn good teacher and I get a lot of compliments. And that didn’t change in the move to remote. Students who had no idea who I was still thought I was and only saw me on Zoom a couple hours a day liked me a lot better than their last math teacher.

However, explaining is my go-to skill. So if that’s you, then not knowing your students might not be something to fear. If you are a beloved mentor whose influence is based entirely on in-class conversations and bonding, or lunchtime safe space, good luck.

One challenge left to take on: I sit my students in ability-level groups and they work together productively. I didn’t try this in summer school. Again, I’m not a huge fan of getting-to-know-you activities. I just bunch the kids together and tell them to get to it. I’ll have to be more conscious about this if I try it on Zoom.

Zoom Breakout Rooms

According to David Griswold, Google Meet has some nice features, but the list of limitations he rattled off have convinced me Zoom is my bet. I learned about breakout rooms in my other summer job, teaching test prep (they begged me and hey, I could go on vacation and still teach so why not?).

Breakout rooms solved a huge problem I had during the spring, when I ran “office hours”. I had no training on Zoom, just used what I saw. I used to have different groups sign in at different times, based on what topic they needed to learn, and it was a huge hassle. Breakout rooms are fantastic. You can set them up ad hoc.

Downside #1–to the best of my knowledge, you can’t add rooms after you’ve started, so I always create a couple extra.

Downside #2–if a kid drops off the line and comes back on, you might not see it for a while. If you, the teacher, are in a breakout room, you don’t hear the sound alert for a new entry. So learn to check the icon (it will say “1 unassigned”).

Downside #3–you can’t peek in on the other rooms. Remember when you were a beginning teacher helping one student out while right behind your back mayhem was breaking out? It feels like that. Except it’s not mayhem, it’s just kids not working.

Still, these are manageable problems. Breakout rooms are your friend.

Collect work right away

I quit assigning homework nearly six years ago. With remote learning, I’m no longer wandering around the room monitoring student work, seeing their progress. Last spring, I just asked students to turn in work via Google Classroom.

I wasn’t obsessive about it; students could skip turning in some assignments. But some students never turned in anything. I’d bring them in for special sessions and establish their level of understanding. Which was a lot of work, but remember, the kids didn’t have to show up at all last spring so I was in “sell” mode.

I couldn’t hold those extra sessions in summer school even if I’d wanted to. Students met with me every day for at least an hour. If they had questions, I held office hours earlier, and they’d come to those. Most kids were also turning in the homework, but at least 10 of the 30-some students were turning in little or nothing, despite coming to class every day and answering questions, demonstrating understanding.

I finally realized that they weren’t turning in work for the same reason they didn’t do homework–because once school ended, they were done. They didn’t think about class until the next day. In short, the reason that I stopped assigning homework all those years ago was still a really good reason.

So what I needed to do was consider this work classwork, not homework. Once I’d explained everything, I didn’t dismiss the class. “Do assignment 2, problems 1-8. DO NOT LEAVE ZOOM WITHOUT TURNING IN YOUR WORK. I will give you a zero otherwise.”

That worked. For some reason, the same kids who were untroubled by zeros for homework would religiously turn in classwork to avoid a zero.

By the way, reviewing classwork adds hours to my week, in case you think it’s all daily walks and a few zoom calls.

Google Form Quizzes

In the spring, I used a Classkick hack as a quiz delivery system. Classkick is a great way to administer several different quizzes to students–upload the quizzes into classkick, which allows you to generate a unique code. You can then give the quiz codes to student groups. Classkick’s value-add is the ability for a teacher to share a quiz view with just one student to help them out with questions.

These were just freeform quizzes, suitable only for regurgitation of the basics. That’s all I was able to do in the spring, and I began summer school using that method as well: build my quiz, convert to PDF, upload versions to Classkick.

But Google Classroom offers a Google “Quiz” option, which I learned was just a google form. With a bit of research, I was able to create my“multiple answer” tests:

Exponents:

Algebraic System

Graphed System

I can weight questions, import images, use images in answer choices. It’s very flexible. Not as flexible as paper and pencil tests, alas. I haven’t yet figured out how to allow students to correct answers or if I want to do that. But it’s a start.

None of this is great.

Pacing is incredibly slow. I’m not optimistic about returning to even my notoriously limited curriculum. If you know a teacher who is bragging about covering everything, that teacher has highly motivated and capable students or a lot of lost kids.  I hate being reduced to one mode of instruction. I know kids are only paying partial attention. their lives have been reduced to nearly nothing. This is a horrible way to teach, a worse way to learn, and shame on the people who think covid19 is a reason to shut down schools.

It’s a terrible thing that fearful people are doing to society, to children, to education. And I’m one of the lucky ones.

 

Evaluating vs Solving

Most math teachers start their year with algebra review. I like the idea of “activating prior knowledge“, as it’s known in ed school, but I never want to revisit material as review. It’s so….boring. Similarly, others “reteach” students if they didn’t understand it the first time and again, no, I don’t do that.

The trick is to wrap the review material in something new, something small. It’s wrapping, after all. For example, suppose the kids don’t really get Power Laws 1, 2, and 3 the first time you teach them, even though you went through them in insane detail and taught them both method and meaning. But you give them a quiz, and half the class is like, what means this exponent stuff? so you grit your teeth, yell at them, flunk most of them on that quiz, and go onto another topic for a week or so. Then one morning write ¾ on the board and ask “How would I write this with exponents?” and through the explanation you take them back through all of the power laws.

But I’m not here to write about power laws, although if you want advice on the best way to teach them, even if it takes longer, there’s no better tutorial than Ben Orlin’s Exponential Bait and Switch.

I’m here to explain how I integrate what we usually call “algebra review” into my course, while additionally teaching them some conceptual stuff that, in my experience, helps them throughout the course. Namely, teach them the difference between evaluating and solving functions for specific values.

Evaluate–what is widely recognized as “plugging in”. Given an input, find the output. Evaluate is Follows P E MD AS rules–well, technically P F MD AS, but who can say that? Note–I am pretty sure that “evaluate” is a formal term, but google isn’t helpful on this point.

Solve–well, technically it’s “plugging in for y”, but no one really thinks of it that way. Given an output, find the input(s).  Follows the rules of Johnny Depp’s younger brother, SA MD E P. (I hope I retire before I have to update that cultural reference). And really, it’s SA MD F P, but again, who can say that?

Things that get covered in Evaluate/Solve:

• Remind everyone once more that addition/subtraction and multiplication/division run left to right, not one before the other. SAMDEP reinforces that, as I put the S first for the mnemonic.
• “Evaluate”–Evaluating purely arithmetic expressions is middle school math.  At this stage of the game, the task is “evaluate the equation with a given value of x”.
• “Solve” –Solving is, functionally, working backwards, to undo everything that has been done to the input. Right now, they know how to “undo” arithmetic and a few functions. They’ll be expanding that understanding as the course moves forward.x
• Hinted at but not made explicit yet: not all equations are written in function format. I believe that, given an equation like  3x + 2y = 12 or x² + y²=25, the terminology is “given x=4, solve for y” or “given y=3, solve for x”, but I’m not enough of a mathie to be sure. Feel free to clarify in the comments.
• As I move into functions, this framework is helpful for understanding that evaluating a function must have one and only one answer, whereas solving a function given an output can have more than one input. It’s also useful to start capturing the differences between absolute value and quadratics, which aren’t one to one, and lines and radicals, which are.
• The “PE” in PEMDAS and SAMDEP stands for exponent, but in fact the laws must be followed for every type of function: square root, absolute value, trigonometry, logs,  and so on. Informally, the “E” means “do the function” or “undo the function”, depending on whether evaluating or solving. So evaluating y=4|x-5| -6  with x=1 means subtract 5 from 1 (the “parenthesis), then take the absolute value (the “exponent”), then multiply by 4 and subtract 6. Solving the same equation would be adding 6, dividing by four, then undoing the absolute value to create two equations, then adding five in each one. (This is more complicated in text than explaining it with calculations on a promethean.)
• YOU CAN’T DISTRIBUTE OVER ANYTHING EXCEPT MULTIPLICATION. This one is important. Kids will change 2(x-1)²  to  (2x-2)² to 4x-4  with depressing speed and while many of them will make the last mistake in perpetuity, I’ve found that I can break them of the first, which also helps with 3|x+5| not turning into|3x+15|. For some reason, they never distribute over a square root, but plenty will try to turn 3cos(3x) into cos(9x).

Here’s a bit of the worksheet I  built.

I have found this prepares the groundwork for an indepth introduction to functions, which is my first unit. So when they’ve finished Evaluate and Solve, followed by Simplify ( more on that later), the functions unit:

• Definition of a function
• Function notation
• Function Transformation
• Parent functions–I start with quadratic, square root, absolute value, and reciprocal, and some of my approach is at the bottom of this article.

So by the end of the unit the students can graph f(x) = 2(x-1)² – 8 , as well as find f(3) and a if f(a)=10, and understand that the x and y intercepts, if they exist, are at f(0) and f(x)=0. They can also do the same for a square root or reciprocal function. Then I do a linear unit and a quadratic unit in depth.

Function notation, particularly f(a)= [value], is much easier for the students to understand once they’ve worked “evaluate” and “solve” with x and y.

This also helps the students read graphs for f(4) or f(z)=7.

Back in January, a Swedish guy living in Germany, as he describes himself, read the vast majority of my blog and then summarized his key takeaways and some critiques. His 6 takeaways are a pretty good reading of my blog, but he’s completely dismissive of my teaching and pedagogy, saying I’m mathematically naive and often, due to my ignorance, end up creating more confusion teaching needless information to my students. He explicitly refers to The Evolution of Equals and The Product of Two Lines, but I suspect he’d feel similarly about The Sum of a Parabola and a Line and Teaching With Indirection.

I’m really sure my students aren’t confused. I get pretty decent feedback from real mathematicians. There are legit differences between teachers on this point that approach religious wars, so there’s that.

Besides, these sort of lessons do two things simultaneously. They give weaker kids the opportunity to practice, and the top kids get a dose of the big picture.

Yes, it’s been a while since I’ve written. Trying to fix that.

 

Learning Styles

 

How widespread is belief in learning styles? There have been surveys in many other countries, but not the US…until now. And this one is very tightly put together. (spoiler: belief is v high). https://t.co/sB0Ef96hy3

— Daniel Willingham (@DTWillingham) May 30, 2019

Isaac Asimov’s third robot story, “Reason“, has all the hallmarks of his early work: painful stereotypes, hackneyed dialog. Still, the conflict it explored has always hooked me.

Powell and Donovan, two troubleshooters who fix puzzling problems with experimental robots, are stuck on a remote sun-mining station training a new robot to capture energy from a planet’s nearby sun, run it through an energy converter, and direct it back to the planet. The robot, QT-1, or Cutie, decides that these humans are naturally inferior and must be early models that his superior frame and brain are designed to replace. His world was the station, his god was the Energy Converter, known as the Master, who wanted Cutie to direct beams to the dots. Powell and Donovan try to convince Cutie that the dots are planets, that he is a robot created by humans to do their bidding. Cutie thinks this is absurd and creates his own cult of believers, indoctrinating all the robots on the station with the will of the Master, with  Cutie as the Prophet. Powell and Donovan worry themselves sick with aggravation and fury.

The tale reaches a climax when Donovan spits on the Energy Converter. Cutie is horrified and angry at the sacrilege and refuses to let the two men into the Operations room. Powell and Donovan see a dangerous asteroid storm coming,  a catastrophic event that could cause the energy beam to misdirect and incinerate a third of the planet. Desperate to convince Cutie of his wrongthink, they hit on the idea of building a robot from the box, as it were. They uncrated a spare robot,  disassembled into parts, and spent three hours painstakingly putting the robot together. See? They created the robot! Just like they created Cutie!

Cutie shakes his head. Silly weak humans. Of course, they assembled the parts. But how did the parts get to the station? Only the Master could achieve that. So he turns away and ignores the two men, who stop sleeping and eating in sick anxiety over the incoming storm and the annihilation it will pour down on earth.

When, after the storm, they are finally released into the Operations room, Powell and Donovan rush in to assess the devastation. But no! Cutie protected all the humans on Earth perfectly and kept the energy supply constant. Or, as Cutie describes it,  Cutie “obeys the will of the Master” and keeps the beams directed to the right place on the dots.

Powell and Donovan realize they were worried for nothing. They just have to bring all the robots be indoctrinated in the Will of the Master as told by the Prophet (that is, trained by Cutie)  and the stations will be run beautifully. Cutie waves goodbye to them regretfully, knowing they are bound for “dissolution”, but encourages them to believe they are going to a better place.

tl,dr: If learning styles make no difference in outcomes, who the hell cares what teachers believe?

Memorization or Learning?

I originally started to write a post on a memorization technique I’m using for the unit circle, and went looking for representative jeremiads both pro and con. Instead, I found Ben Orlin’s piece When Memorization Gets in the Way of Learning (from five years back):

…which is the opposite of a standard, boring piece and serves as a good counterpoint to explain some recent shifts in my pedagogy.

It’s a good piece. In many ways, the debate about memorization runs parallel to the zombie problem–students regurgitate facts without understanding. Ben’s against that. Me, too. Ben says that testing requirements create tensions between authentic learning and manageable tests; I have various means of ensuring my students understand the math rather than just hork it up like furballs of unknown origin, so am less concerned on that point.

But I don’t agree with this sentiment as much as I probably did a decade ago: Memorizing a list of prepositions isn’t half as useful as knowing what role a preposition plays in the language. 

Not in math, anyway.

 

A couple years ago, after I’d taught trigonometry two or three times, I suddenly noticed that at the end of the year, my students were very fuzzy on their unit circle knowledge. (It’s no coincidence that Ben’s article and my observations are both focused on trigonometry, a branch of math with a significant fact base.) When working trig equations, they’d factor something like the equation above, use the Zero Product Property, solve for sin(x)…and then stop.

“You’re not done,” I’d point out. You’ve only solved for sin(x). What is the value of x?”

Shrug. No recognition. My tests are cumulative. Many students showed significant recall of concepts. They were using ratios to solve complex applications; they were sketching angles on the coordinate plane–both concepts we hadn’t revisited in months. They could sketch the unit circle from memory and eventually figure out the answer. But they had no automatic memories of the unit circle working backwards and forwards, even though I had emphasized the importance of memorizing it.

Upsetting, particularly at the end of the year. The name of the class is Trigonometry, after all. Solving for sin(x) requires not one tiny bit of trig. It’s all algebra. Trigonometry enters the picture when you ask yourself what angle, in radians or degrees, has a y to r ratio of 1 to 2.

The sine of π/2 is not among [the important things to memorize]. It’s a fact that matters only insofar as it connects to other ideas. To learn it in isolation is like learning the sentence “Hamlet kills Claudius” without the faintest idea of who either gentleman is–or, for what matter, of what “kill” means.

Well, okay, but….if a student in a Trig class can’t work a basic equation without a cheat sheet, what exactly has he learned? He already knew the algebra. Does the same standard hold for SOHCAHTOA, or can I still assume the student has successfully learned something if he needs a memory aid to remember what triangle sides constitute the sine ratio? What else can be on the cheat sheet: the Pythagorean Theorem? The ratios of the special rights?

Ben describes memorization as learning an isolated fact through deliberate effort, either through raw rehearsal or mnemonics, both of which he believes are mere substitutions for authentic learning. He argues for building knowledge through repeated use.

Sure. But that road is a hard one. And as Ben knows much better than I, the more advanced math gets, the more complex and numerous the steps get. Most students won’t even bother. Those who care about their grades but not the learning will take the easier, if meaningless route of raw rehearsal.

So how do you stop students from either checking out or taking the wrong road to zombiedom?

I’ve never told my students that memorization was irrelevant, but rather that I had a pretty small list of essential facts. Like Ben, I think useful memorization comes with repeated use and understanding. But what if repeated use isn’t happening in part because of the pause that occurs when memory should kick in?

So I’ve started to focus in on essential facts and encouraged them to memorize with understanding. Not rote memorization. But some math topics do have a fact base, or even just a long procedural sequence, that represent a significant cognitive load, and what is memorization but a way of relieving that load?

The trick lies in making the memorization mean something. So, for example, when I teach the structure of a parabolas, I first give the kids a chance to understand the structure through brief discovery. Then we go through the steps to graph a parabola in standard form. Then I repeat. And repeat. And repeat. And repeat. So by the time of the first quiz, any student who blanks out, I say “Rate of Change?” and they reflexively look for the b parameter and divide by 2. Most of them have already written the sequence on their page. The memorization of the sequence allows them repeated practice.

But it’s not mindless memorization, either. Ask them what I mean by “Rate of Change”, they’d say “the slope between the y-intercept and the vertex”. They don’t know all the details of the proof, but they understand the basics.

I take the same approach in parent function transformations, after realizing that a third of any class had drawn parent functions for days without ever bothering to associate one graph’s shape with an equation. So I trained them to create “stick figures” of each graph:

I drew this freehand in Powerpoint, but it’s about the same degree of sloppiness that I encourage for stick figures. They aren’t meant to be perfect. They’re just memory spurs. Since I began using them a year ago, all my students can produce the stick figures and remind themselves what graph to draw. They know that each of the functions is committed on a line (to various degrees). Most of them understand, (some only vaguely), why a reciprocal function has asymptotes and why square root functions go in only one direction.

So did they learn, or did they memorize?

I haven’t changed my views on conceptual learning. I believe “why” is essential. I’m not power pointing my way through procedures. I am just realizing, with more experience, that many of my students won’t be able to use facts and procedures without being forced to memorize, and it is through that memorization that they become fluid enough to become capable of repeated use.

Like Ben, I think a zombie student with no idea that cosine is a ratio, but knows that cos(0) = 1, has failed to learn math. I just don’t think that student is any worse than one who looks at you blankly and has no answer at all. And addressing the needs of both these students may, in fact, be more memorization. Both types of students are avoiding authentic understanding. It’s our job to help them find it.

So I’ll give an example of that in my next post.

Great Moments in Teaching: The Charge

Friday, two weeks from the end of school, and it’s rally schedule: chop off fifteen minutes from each block for a screaming session in the gym. It’s fourth block, my trig class, and although I try not to have favorites, this semester has been a bit low on students with energy and ability. But even the goof-offs in this class can remember the basics of trig, have put some effort into memorizing the unit circle, reciprocal values, the occasional Pythagorean identity,  know the difference between sine and cosine graphs.  And only two cheaters. The top kids are amazing, enthusiastic, and driven–and there are lots of them, many of whom I just taught Algebra 2.  So a fun class, and really the only one with a genuine personality this semester.

I had given them some extra time to finish up a test from the day before, and it’s now just 35 minutes to rally.

“OK, I want to cover a couple things to set up Monday. Let’s….”

“NOOOOOOO!!!!” the blast of complaints hit me. I turned around and glared.

“Come on! It’s Friday! You can’t make us learn something new!” Tre, who last had a math teacher that wasn’t me in freshman algebra, put on his most ingratiating grin.

“It’s so hot, and my brain hurts. Please, no more math!” Patti slumped dramatically.

“QUIET!” I turned back from drawing a cosine graph to bellow them into submission.

“I just want to introduce a couple of interesting properties and get you thinking, once again, about…oh, for christ’s sake.”

“WHAT??? What happened?” the students crane their heads forward to see the object of my irritation. I was growling at a student whiteboard sitting on a desk.

“Oh, some student used a fricking sharpie to draw a self-portrait.” and I held up the board so the class could see the penis.

“HAHAHAHAHA!” TJ was cracking up and I whirled at him furiously.

“You know, we use these white boards every day, and if I can’t get the sharpie off, it’s ruined. You think it’s FUNNY that students destroy my stuff?”

TJ was genuinely puzzled. “No. You just called him a dick. Like, without saying so. That was cool.”

“Fine. Ruin the fun of yelling at you. Take one more ounce of joy from my day.” I grinned at him and sprayed cleaner on the board.

“Ain’t no cleaner taking off sharpie,” Ahmed sympathized.

“Dude, this is Kaboom,” Tre said. “Kaboom’s the bomb.”

“Best cleaner in the known universe.” I spray the board and let it sit. All my kids know I love Kaboom. I tell new teachers about Kaboom, an essential teaching tool. When the kids write F*** in Sharpie, it’s so incredibly satisfying to wipe the obnoxiousness out of existence with one spray. Lesser challenges–gang graffiti, pencil sketches, soda spills, even small patches of gum–all disappeared.

“I hate students, dammit.” I turned back to the board. “I mean, don’t get me wrong. I love you all. But I just hate students. Ruin my stuff, treat it like crap….” I stop, because students breaking my stuff can put me in a foul mood in a hurry.

“It wasn’t us!” Matteo protested.

“Dude, it was you.”

“Screw you, Furio, how do you know?”

“Cuz you’re a dick! That’s your picture!”

I laughed, feeling much better. “Look, back to work. So you know how there’s a line, and then we can square a line, or multiply it by another line, to get a…”

“Parabola,” a reasonable amount of the class chorused, but I could hear talking.

“Shush, whoever’s talking. What happens when we square the cosine function? Take a look at the function and let’s just square what we….BE QUIET BRIAN..see. Cosine starts at…QUIET.” I turn around, wait for quiet. “Cosine starts at what, Furio?”

“1.”

“So 1 squared is..?”

“1”.

I mark (0,1) in a different color, and move to the next hashmark. “Cosine is zero at pi over 2, zero squared is…QUIET.”

Most kids were paying attention, but there was this low level nattering that rose up every time I turned to the board.  But we got through the first one quickly.

“So here’s the square of the cosine function. What do you notice?”

“It’s a cosine graph!” Vicky.

“Sure looks like it. Period? Amplitude?” and we identified all the parameters for a cosine function graph.

So the square of the cosine function can also be expressed as a regular cosine graph. Amplitude and vertical shift, one half, period one half the usual.”

Ahmed said with faux judiciousness, stroking his chin, “Ah, but how do we know this? It might just look like a cosine graph!”

“Good question. We can see the key points work, but maybe that’s just a coincidence. So pick a value and let’s plug it in. QUIET!”

“How about pi over six?”

Carla was impressed. “Wow, when you double the value, it becomes something entirely different.”

“Yes….QUIET!!! I’m always surprised at how the alignments happen. So now let’s go on to the sine function. What do you all think will happ….QUIET!”

“Jesus Christ, Eduardo and Brian, will the two of you shut.up.? NO! Stop the innocent ‘who me?’ crap. Three times in the past three minutes. I tell you to be quiet, turn to the promethean, turn around and there you are yapping again. Do I need to move you?”

Eduardo (Manuel‘s younger brother) and Benny look abashed, hearing the edge in my voice. I was mad at myself more than anything these two had done. Note to new teachers: don’t push through without attention. Constantly shushing is a sign you don’t own the room..  Don’t push through, stop when you need to. And it wasn’t an accident I’d picked two of the top kids in the class to shut down; it showed everyone else I was serious, if the unusual edge in my voice wasn’t enough.

By now I was furious with myself, and boy, do I get global in a hurry. My rotten students ruin my whiteboards and never shut up. I’m an idiot who decided to teach something complex 30 minutes before the weekend. And there are times when I’ve decided it’s not worth it and call it quits–call a pop quiz, put a problem on the board as an exit ticket, something. But deep breath, act like nothing happened, and push on, vowing to give it one more shot before I bail on an exit ticket activity.

“Wait.” Joanie, probably my top math student this year, sat up and scowled at the graph dots. “How can that be a cosine, too? That’s weird.”

“What kind of cosine function? What’s different?”

“It’s reflected. So cosine squared is cosine, and sine squared is negative cosine?”

“Looks like it.”

“But what’s the point of this?” Vicky asked. “Since squaring a sine or cosine function just takes you back to cosine, why do it?”

“Well, math applications will quite often require you to square functions, so it’s good to know how they behave. However, I really just want you to think about exploring functions. Up to now, you’ve been working primarily with transformations or known formats with parameters you can just plug in. But now we’re investigating functions that aren’t familiar with. Notice, too, that we did this all graphically with a minimum of evaluation.”

“So just for fun, what if we add the two functions we just created?”

“Here they are together. So let’s add the five primary points.”

TJ puzzled. “They’re all one? Really? That’s weird.”

“Yeah, but you can see it in the graphs,” Juan observed. “They’re equal at one-half, at opposite ends at one.”

I join all the points.

“So the graph y= cosine squared plus sine squared is always….”

“One!” the class chorused.

And then I threw out casually, oh so casually, “And cosine squared plus sine squared is…”

“One!…”

The pause was the best part. I looked down, and waited as the recognition grew, until by god, the entire room was shouting in approval, clapping and stomping.

It’s one of those things that maybe you had to be there. But in half an hour, at the end of a day, in hot weather, right before a rally and a weekend, I’d not only gotten those kids to apply their knowledge of trig graphs in a new approach, but draw a connection from graphic to algebraic. They hadn’t recognized the familiar equation because their minds were in “graph” mode, and only when I asked about a Pythagorean identity, using almost exactly the same words, did they realize that they already knew what the graph would show. But not until then.

And they thought it was really cool that I’d pulled them around to this recognition.

Literally, a minute of stomping until I waved it down. “All right! Thank you. Remember during the first week, when I told you I’m a stickler for understanding the connection between algebraic and visual representations? Here you go.”

And then, “But what about tangent? What happens when you square that?”

Ten minutes left and I’ve got them asking questions. I realized I haven’t had to shush them once.

And just as the bell rings, we established that tan²(x) + 1 = sec²(x).

The kids rushed out to the rally. Rallies are my one Bad Teacher thing: I don’t go. I checked the whiteboard, Kaboom had wiped out most of the damage. Then I walked to Starbucks just completely charged, reliving the math and the applause. All the yelling, all the grouchiness, wiped away. I’d killed.

I keep telling you: Teaching is a performance art.

 

Four Obvious Objections to Direct Instruction

Recently, I defended teachers from Robert Pondiscio’s accusatory fingerpointing. Why no, sir, twas not teachers at the heart of the foul deeds preventing DI’s takeover of the public schooling system.

I don’t have any great insights into why DI isn’t more popular. But any reasonable person should, without any research, have several immediate objections to accepting the Direct Instruction miracles at face value. Hear the tales about Project Followthrough and spend ten minutes reading about this fabulous curriculum, and a few minutes thought will give rise to the following obstacles.

The weird objection

I’ll have more to say later, hopefully, about the roots of Direct Instruction. But no research is necessary to see the B. F. Skinner echoes.  Direct Instruction looks much more like conditioning than education.  A curriculum sample (I can’t make it bigger, click to enlarge):

You’re thinking good heavens, those “signals” are just optional, right? Nope. This video , without prompting, tells the viewer that yes, “signals” are required.

Recently Michael Pershan observed that ” while schools are primarily in the business of teaching kids as much as we can, it’s not anyone’s only priority. There are other things that teachers, administrators, parents and kids value besides instructional efficiency.”

Yes. Many of us value public schools that don’t feel like a cult.

The age objection

From the meta-analysis that’s given rise to all the recent stories:

The strong pattern of results presented in this article, appearing across all subject matters, student populations, settings, and age levels, should, at the least, imply a need for serious examination and reconsideration of these recommendations.

It’s behind a paywall, but I can’t help but be skeptical. I’ve never heard of Direct Instruction implementations at high school.  High school is leagues harder than elementary school and middle school. How would DI work?

Teacher script: “Hamlet Act One Scene One Word One What Word?”
[tap]
Class: “Elsinore!”

Or math:

Teacher script: “Y=mx + b is the slope intercept form. Word m What Word?”
[tap]
Class: “Slope!”
Teacher: “Word b What Word?”
[tap]
Class: “Intercept!”

How many subjects have been broken down to that level? How many books have they scripted for instruction? Or is the high school curriculum like this US History sample, a few questions every paragraph?

I don’t know. I’d guess the researchers don’t know, either.

If DI’s curriculum isn’t entirely defined for high school students in all subjects, then how can the claim be made that DI works for all age levels?  How can we be sure that the gains made in elementary school aren’t subject to the dreaded fadeout? What if DI is simply a good method of teaching basic skills but won’t address the gaps that arise in high school?

Maybe answers–good answers, even–exist, maybe DI works for fifteen to eighteen year olds, maybe Romeo and Juliet can be broken down into tap-worthy chunks. Or maybe those writing paeans about Project Followthrough have no success stories about older kids to tell.

The money objection

There’s a new meta-analysis [that] documents a half-century of “strong positive results” for a curriculum regardless of school, setting, grade, student poverty status, race, and ethnicity, and across subjects and grades.–Robert Pondiscio(emphasis mine)

If it works for all income levels, why aren’t rich kids using it?

I mean, surely, this incredible curriculum is what they use at Grace Church School or Circle of Children to teach these exclusively and mostly white little preschoolers how to read. Distar is the gold standard at  exclusive Manhattan elementary schools. All the teachers are going word one, what word? (tap) and all the little hedge fund progeny obediently repeat the word, or Word.

Except, of course, that’s not the case at all. Check all the websites and you’ll see they brag about their inquiry learning and discovery-based curriculum.

 

Zig Engelmann has written that he focused his attention on the “neediest” children, but that his curriculum helps all students achieve at the highest level. In which case, Zig, go sell your curriculum to the most exclusive private schools. Public schools spend much time arguing that poor children deserve the same education rich children’s parents pay for.

The race objection

I almost left this section out, because it is necessarily more detailed and less flip than the others. At the same time, I don’t see how anyone can hear about DI the miracle and not ask about race, so here goes.

About thirty years ago, Lisa Delpit wrote a stupendous essay, The Silenced Dialogue that just obliterated the progressive approach to education, effectively arguing that underprivileged black children needed to be directly taught and instructed, unlike the children of their well-meaning progressive white teachers.  As I looked up her article to cite  her comments about the “language of power” I realized that Delpit actually discussed this using the context of Direct Instruction (Distar is the primary Engelmann brand):

Note that Delpit, who so accurately skewers progressives for withholding the kind of information that black children need, then rejects the notion of “separating” students by their needs.

She wants it both ways. She wants to acknowledge that some kids need this kind of explicit, structured curriculum while denying the inevitable conclusion that other kids don’t.

DI claims that all kids, regardless of race, see strong improvements.  But take a look at the videos, like this one from Thales Academy, and notice all the students reciting together. They all learn at exactly the same pace?

 

Really?

So I’m going to spoil alert this one. A quick google reveals that Direct Instruction doesn’t allow a student to progress until he or she has mastered the level, and yes, there is ability grouping.

History suggests that the students who move forward quickly will be disproportionately white and Asian, while the students who take much longer to reach mastery will be disproportionately black and Hispanic.

In fact, public schools are strongly discouraged from grouping by ability, and by discouraged I mean sued into oblivion. So how can Direct Instruction achieve its great results without grouping? And if DI helps all races equally, then won’t the existing achievement gap hold constant?

It’s quite possible that DI is an excellent curriculum for at risk kids, particularly those with weak skills or a preference for concrete tasks. It’s not credible that DI instituted in a diverse school won’t either lead to very bored students who don’t need that instruction or the same achievement and ability gaps we see in our current schools.

As I said, these are the relatively straightforward objections that, I think, make a hash out of Robert Pondiscio’s claim that teachers, those foul demons of public instruction, were the source of all DI discontent.  Next up, I’m going to look at some of the actual data behind the claims.