What I Learned: Year 3

I want to continue my teaching retrospective, if only for my own edification. Year 3 in particular led to major changes in my curriculum and pacing.

To recap: my first year was spent in a very progressive school, where I taught algebra, geometry, and humanities, both literature and history. I loved teaching, didn’t much care for the school, and definitely wasn’t sufficiently of the left to stay there. Years 2 and 3 were at a Title I school, 65% Hispanic/ELL. As I’ve said before, year 2’s all algebra all the time schedule was my toughest schedule ever as a teacher; I do not expect to see its like again. Which is good, because I still get flashbacks. I have, in fact, never officially taught algebra 1 since that time although most people would consider what I teach in Algebra 2 to be, in fact, Algebra 1.

Year 3 was at the same school, but I was assigned Algebra 2 and Geometry. And that made all the difference.

Establishing Classroom Ambiance

My 65 geometry students included twenty I’d taught the previous year in Algebra I, students who knew and liked me.

First day, I started one class a bit early when in walked Robbie, redheaded, pale, anxious, diagnosed with Asperger’s but almost certainly a high functioning autistic. I told him to have a seat, and didn’t immediately realize that the little freshman was utterly aghast at the idea that he was late to class. He was murmuring “class starts at 9:15, I was here at 9:12” over and over again, slowly working up to a meltdown by the time I noticed. Before I could react Augustin, a junior, first student I’d met at this school the year before, leaned over from a desk in the same group.

“Relax. Teacher started early. Never cares about time anyway. You’re good.”

Meltdown over. Robbie was awestruck that a junior had deigned to notice him. He also remembered all year that I “never cared about time”, which did much to keep him balanced and happy with a teacher incapable of a predictable routine. I have always remembered Augustin for his offhand kindness to an odd kid.

My geometry classes gave me the feeling of being a known quantity, a teacher with student cred, something I’d long easily established in my Asian enrichment classes, as well as my Kaplan test prep, but never felt in a public school before. I’d always been a loose disciplinarian, an easy classroom controller, and this isn’t as easy in test prep as you might think—it’s why I got so much work. I knew that teaching outside of private instruction would be different, but I found the change more challenging than I expected.

For my first two years in public school, I struggled to recreate the friendly “we’re all in this together” atmosphere I expected to achieve easily. My first year, only my humanities class ever achieved the ambiance I took for granted in private instruction. Only two of my 4 algebra classes (one was a double block) had that cheerful noisiness that is now a trademark of my public school classes. I wasn’t a failure as a teacher; in many ways, I was doing exactly what I anticipated and dealing with expected obstacles. But I had secretly mourned the loss of my standing as a popular teacher. And now, suddenly, I had my mojo again.

My algebra 2 classes were more like my algebra 1 classes from the year before; I didn’t have yet the same easy rapport that I had with my geometry students. This gave me a chance to study the difference. Would I always need to have repeat students, or was there something I could do to establish the environment of easy fun with hard work–or at least some effort?

Over time, I learned that some students find me harder to understand than others. They often don’t grok my ironic asides. They do not understand that I “blast” without malice. They assume I hold grudges, that I count misdemeanors in a black book somewhere. They don’t understand I am often somewhat ruthlessly focused on one objective. As I’ve said before, teaching is a performance art, and the act of engaging students to convince them to learn is often an arduous mental task.

And so I’ve learned to explain this up front. That I am often sarcastic, and think attempts to ban this essential classroom management tool are Against God. That I’m not often annoyed, and usually harmless. But when I am annoyed I yell first, ask questions later when I remember to, which I often don’t. That I am unlikely to remember what I was mad about 20 minutes later, much less hold a grudge. In fact, the only behaviors that I remember are cruelty and cheating. That I love teaching, and like all of them. Except Joe. I can’t stand Joe. And frankly, I’ve never been a big fan of Alison. But except them. And Mario. Don’t care for Mario much. But everyone else. Really. (Yeah, see that, kids? Mild irony. Get used to it.)

I’ve also learned to reach out on things that don’t matter as much to me but I’ve realized matter much more than I realized to students. I’ve always been one to say “Hi!” in the hallways and chitchat for a moment with past and present students but in truth honestly don’t care about football games or sporting events. Still, kids really do like it when you show up at the games, or ask about the outcomes, or call out a student who had a great game or ran a PR. I ban the singing of Happy Birthday because the noise is unbearable, but after they beg, I give them a count of three and we all shout the phrase at once. And all my classes delight in realizing how easy it is to drive me off-topic by asking about food or politics.

All my ability to deliberately set a classroom environment came from the lucky break of teaching geometry to some of the same students I’d just passed in algebra.

Coverage vs. Comprehension

I sure hope Bud Blake got credit for this 1974 classic, reproduced daily in ed school and professional development lessons everywhere.

I used to take state tests more seriously, and was quite proud that my first year out, I “hit the dinger” in geometry and algebra. I hadn’t rushed, and even back then had deemed many topics non-essential, or at least far less important than others. My students were doing reasonably well on tests, which were free-response that year.

But towards the end of the year, I realized with a shock that many of my mid-tier students had forgotten most of the content. Students who understood the Pythagorean Theorem were now marking up triangles with SOHCAHTOA when they had two sides and just needed the third. Algebra students were plugging linear equations into the quadratic formula. Cats were sleeping with dogs. All was not right. It was as if they’d never been taught.

Year two, I was primed to look for learning loss but pacing was so impossible with the wide ability range that I instituted four levels of differentiation. I succeeded in slowing down instruction and letting students absorb more information.

But year three saw my first attempts to help Stripe learn to whistle.

In geometry, the first sign of change came in October. I’d explained transversals of parallel lines. I’d done a great job. Brilliant, even. Not content to simply lecture, I asked questions, prompted discussion, ensured students saw the connection and sketched the familiar representation.

And the lesson didn’t thud. All the students obediently worked the problem set. They asked reasonable questions.

So I don’t know, really, what compelled me to double check.

“Am I picking up a weird vibe? You all are working, but I have this sense that you’re still confused.”

Murmurs of agreement.

“How about everyone close their eyes and we’ll do a thumb check?” (I rarely use such obvious CFUs these days, but they’re still a great tool for uncertain situations.)

Most of the thumbs came up sideways.

So I told the kids I’d think about this for a while, and came back with an activity, one that required about $70 in materials that I still use to this day.

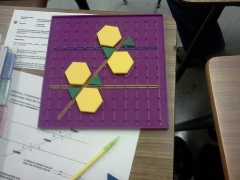It worked. The transversal angle relationships were easier to understand with the physical representation, the students could see the inevitability, see how the angles “fit”. And from that point, they could easily see that unless the transversal was perpendicular, each transversal over parallel lines formed only two distinct angle measurements: an obtuse and an acute.

A nifty transversal lesson wasn’t the important development, even though my geometry students still enjoy the activity almost as much as they enjoy creating madcap patterns with the boards and rubber bands.

Sensing confusion despite a generally successful lesson, I had developed an illustration on my own to develop a stronger understanding. I was beginning to spot the difference between teaching and learning.

I still struggle with this. It’s very easy to get sloppy, particularly in a large class with ability ranges of 4 to 5 years, with kids in the lower ranges happily sleeping through classes, stirring themselves only enough to beg me for a passing grade. But ultimately, I circle back with yet one more pass through, coming up with an illustration or series of problems to shine a light on confusion.

I’ve written extensively of Year 3’s other major development. Faced with the reality that I’d wasted a semester covering linear equations and quadratics that students didn’t remember in the slightest, I decided to start over, beginning with modeling linear equations. Not only did I completely change my approach to curriculum, I also flatly punted on coverage from that point on, focusing on the big five for every subject. As I improve at introducing and explaining concepts, my students become capable of taking on more challenging topics; the interaction between my curriculum and student understanding is very much a positive feedback loop.

Ironically, my decision to abandon coverage was driven in part because Algebra 2 was a terminal course, meaning it was to be offered only to remedial seniors, students were not expected or in fact allowed to take any other math course. For this reason, I felt free to craft my own course to focus purely on getting the students ready for college math. But at least half of my students were juniors, and most of them took pre-calc the next year. This was my first exposure to Algebra 2’s dual nature. More on that later.

Mentoring Colleagues

For my first two years, I had almost no contact with colleagues. Year 3, two new math teachers joined and we instantly hit it off. Went for coffee on late start mornings, beers after work. I was their resource; both of them found me far more helpful than their assigned mentors. I still meet up with both of them four or five times a year at least.

I left that year for my current school, and went over two years again without any real colleagues. I missed it. Having spent most of my professional life working without colleagues that liked lunch, beer, coffee, whatever, I can map out the exception eras, and treasure them. Last year I began mentoring, and now have lunch, coffee, whatever with them individually and together.

I’m not chummy enough, much less normal enough, to bond easily with other teachers. But I’m a good mentor, and that seems to be how I make friends as a teacher.

Finally, Year Three taught me how to cope with genuinely unfair treatment, which I haven’t often had to deal with. I never go into details about it, but while I wasn’t crazy about the school, I didn’t want to look for jobs again. Being a fifty year old teacher without a job is a Very Bad Thing—of course, take out the word “teacher” and it’s still true, probably more so.

On the other hand, while I wasn’t crazy about that school, I am very happy at this one. What do they call that, perspective?

On the Spring Valley High Incident

So the Spring Valley High School incident is yet another case of a teenager treating a cop like a teacher. This is, as always, a terrible idea.

I watch the video and wonder about the teacher. I wonder if he’s wondering what I’d wonder in his shoes. Teachers aren’t just focused on the recalcitrant girl who refuses to comply, who hits the police officer, who gets arrested. Teachers notice the girl directly behind the cop and the defiant kid, the one who wasn’t a troublemaker, was just sitting in class doing her work and nearly gets clobbered by the flipped over desk. Or the other kids trying not to watch–suggestion, I think, that the shocking events aren’t a common occurrence. Teachers notice that the kids are working with laptops and hope none of them fly off a desk into another student. (Teachers probably also notice the photographer’s test has many wrong answers. Occupational hazard.)

He’s got to be wondering, now and forever, if he could have prevented this. One time, a student in my class inexplicably left her $600 iPhone on her desk during a class activity that involved working at boards, and it disappeared, which required a call to the supervisors and a full class search. I told them who I suspected, then left because I didn’t want to know. When I came back, they’d detained the strongest student in the class–not for stealing the phone, which was never found. I have decided it’s better not to say why, but it was one of those things that lots of kids do in violation of policy because they’re unlikely to get caught. But if they get caught, it’s bad. (No, not drugs). He was suspended for the maximum time period and had to worry about more than that, although more was mostly scare talk.

The point is, I felt absolutely terrible. The student who left the phone out was careless and silly, the student who stole the phone was a criminal, the student who got suspended was knowingly in violation of a major school policy without the slightest thought for his long-term prospects. But if I’d just seen the damn phone on the desk, none of this would have happened.

So when I look at this video, like many if not most teachers, I’m not thinking about whether the girl deserved to be flipped about, because that’s the cop’s problem. I’m wondering was there anything that teacher could have done to avoid having the cop there in the first place.

Reports say that the student initiated the event by refusing to turn over a cell phone—also offered up is refusal to stop chewing gum, which I find unlikely. However, it’s clear the student was refusing several direct orders that began with the teacher and moved up through the administrator and the cop.

Defiance is a big deal in high school. It must not be tolerated. Tolerating open defiance is what leads to hopelessness, to out of control classrooms, to kids wandering around the halls, to screaming fights on a routine basis. Some teachers care about dress code, others about swearing, still others get bothered by tardies. But most teachers enforce, and most administrators support, a strong, absolute bulwark against outright defiance as an essential discipline element.

Let me put it this way: an angry student tells me to f*** off or worse, I’m likely to shrug it off if peace is restored. Get an apology later when things have settled. But if that student refuses to hand me a cell phone, or change seats, or put food away, I tell him he’ll be removed from class if he doesn’t comply. No compliance, I call the supervisor and have the kid removed. Instantly. Not something I spend more than 30 seconds of class time on, including writing up a referral.

At that point, the student will occasionally leave the classroom without waiting for the supervisor, which changes the charge from “defiance” to “leaving class without permission”. The rest of the time the supervisor comes, the kid leaves, comes back the next day, and next time I tell them to do something, they do it. Overwhelmingly, though, the kids just hand me the phone, put away the food, change seatswhen I ask, every so often pleading for a second chance which every so often I give. Otherwise, the incident is over. Just today I had three phones in my pocket for just one class, and four lunches on the table that had to wait until advisory was over because I don’t like eating in my classroom.

We have a school resource officer (SRO), but I’d call a supervisor for defiance, and I’ve never heard of a kid refusing to go with a supervisor. If there was a refusal, at a certain point the supervisor would call an administrator, and it’s conceivable, I guess, that the administrator could authorize the SRO to step in. So assuming I couldn’t have talked this student down, I would have done what the teacher did, and called for someone else to take over—and long after I did something that should have been no big deal, this catastrophe could conceivably have happened.

I ask you, readers, to consider the recalcitrance required to defy three or four levels of authority, to hold up a class for at least 10-15 minutes, to refuse even to leave the classroom to discuss whatever outrage the student feels warrants this level of disruption.

Then I ask you to consider what would happen if students constantly defied orders (couched as requests, of course) to turn over a cell phone, or change seats, or stop combing their hair, or put the food away. If every time a student defied an order, a long drawn-out battle going through three levels of authority ensued. School would rapidly become unmanageable.

So you have two choices at that point: let madness prevail, or be unflinching with open defiance. Students have to understand that defiance is worse than compliance, that once defiance has occurred, complying with a supervisor is a step up from being turned over to an administrator, which is way, way better than being turned over to a cop. (Note that all of this assumes that the parents aren’t a fear factor.)

Some schools can’t avoid the insanity. Their students simply don’t fear the outcomes enough, and unlike charters, they are bound by federal and state laws to educate all children. If the schools suspend too many kids, the feds will come in and force you into a voluntary agreement. This is when desperate times lead to desperate measures like restorative justice, where each incident leads to an endless yammer about feeeeeeeeelings as teachers play therapist and tell their kids to circle up.

Judge the cop as you will. I can see no excuse for putting other students in danger; the fight could have seriously injured the girl sitting directly behind the incident. He could have cleared the area first, making sure all students were safe. I believe that’s his responsibility.

However, once the administrator asked the SRO to take over, the student was dealing not with a school official, but with a cop. At that point, she was disobeying a police officer’s order. On government property. And she is clearly hitting him, in this video.

And, like I said, disobeying a cop is a bad idea.

So the question is not what should the cop have done, but why did the administrator call the cop? And what would you have had the administrator do instead? Don’t focus on that single incident, because teachers, administrators, and cops don’t have that luxury. They have to handle it in such a way so that defiance doesn’t become a regular routine, that students customarily obey their teachers, maybe with some backtalk, maybe with ample opportunities to walk a bad mistake back. Ultimately, though, students have to comply. If a school backs away from that line, defiance gets contagious. It’s one thing for new, inept teachers to have trouble controlling their students, quite another for an entire school to give up.

I recently had an exchange with David Leonhardt on his NAEP scores article, and he asked me “I assume you agree school quality should be linked to amount students learn, yes?”

Well, not the way we currently measure it, probably not. But I do think school quality should be linked to established order and by “order” I don’t mean an Eva Moskowitz gulag. Control freaks like Moskowitz fail to allow for normal mood swings and eruptions from kids who are, after all, engaged in an involuntary activity for eight hours a day.

Schools that fail to establish order are those like Normandy High School, with out of control violence, open defiance of teachers and administrators, and students in constant danger of assault. Students should have the opportunity to learn, even if they aren’t mastering material at the rate our policy wonks would allow. Schools that can’t enable that are genuine failures.

The Moskowitz contingent point to schools like Normandy as rationale for their despotic rules. Look, they say. Let “these kids” think they can act however they like, and you end up with screaming, chaotic classrooms, truancy, assaults and fights on and between students, ineffectual teachers, and worst of all, low test scores. Teach them to behave respectfully, five times more compliant than suburban white kids, and you’re doing them a favor, saving them from “those schools”. Better Animal Farm than Clockwork Orange

Any school with a solid percentage of kids who’d really rather be somewhere else has to find a balance. Make enough kids want to comply so there’s room to expel the kids who routinely don’t. This isn’t achieved by Eva Moskowitz tyranny, but nor will restorative justice get the job done. It’s hard. There has to be limits. There has to be balance. Administrators who think they have the perfect mix are probably kidding themselves.

In the meantime, if, like Martin O’Malley or Chris Hayes, you’d be “ripped ballistic” if a cop did this to your kid, familiarize yourself and your children with the dangers of disobeying a cop and resisting arrest.

Braindumping the PSAT: A Few Questions for David Coleman

The day after the first PSAT sitting, two parents (at least, I think they were parents), posted this this exchange
on College Confidential (click to enlarge):

The day of the PSAT carried this slightly more obscure exchange:

Suzyq7’s comment seems to come out of nowhere, because almost certainly the College Confidential moderators purged a post or two. It appears that FutureMMAChamp or some other poster explained that some testers knew exactly what they’d gotten wrong because they had an early copy of the test, which led to Suzyq7’s outburst. That post got purged, so it’s hard to make sense of the conversation, but the gravamen of the charge comes through.

Notice the lack of “what on earth are you talking about?” responses. These posters aren’t being challenged for their grasp on reality.

So on October 4th, someone posted actual PSAT content. No one knew for sure it was PSAT content, I assume, which is why the content remained on the site until October 15th. At that point, it appears, the moderators became aware of the posts and purged them. Or maybe the posts are still online, although lord knows I’m a determined searcher and I can find no record of them. The moderators also deleted or modified posts referencing the content whenever possible.

From October 3rd until some point after October 15th, actual PSAT test questions were readily available on a forum that sees about 2 million unique viewers a month. Then that same forum, with the help of Google, Reddit, Twitter, Tumbler, and other social media sites, provided October 28th testers with a roadmap of all the questions on the test.

You really have to chuckle, don’t you?

All those reporters writing indulgently about the PSAT testers violating their promise to refrain from discussing test questions. Most or all of the tests passage texts have been revealed: Frederick Douglass 4th of July speech, the Jason Goldman’s article on researchers establishing differences between dogs and wolves (images included), and Julia Alvarez’s In the Name of Salome (the one about Herminia and her papa). Brian Switek’s piece on Nasutoceratops, the large nosed horn faced dinosaur or a similar piece was used in the writing section.

Peter Greene of Curmudgucation went so far as to include tweets with images from the test, and thinks it’s a big joke because the PSAT is “a test which everyone takes essentially on the same day” (it’s not. More on that in a minute). But then, Peter tells his students that the “P” stands for “Practice”, so hey. (It’s “Preliminary”, but then, the SAT doesn’t stand for anything any more, so maybe Peter thought he could just invent a P.)

I can only assume that the journalists, idealistic humanity majors sorts, found the tumblr posts creative. They might not have been as thrilled by the more, er, explicit discussions that were taking place out in the open Internet.

For example, the google doc in which participants discuss as many of the questions as the participants can remember. You can check out the original, but my pdf takes less time to load and omits the first page of obscenities. (The first link the author made was apparently deleted by Google as a violation of the terms of service.)

The google doc participants discuss the math and reading questions, with the occasional English query as well. They go into considerable detail; the enterprising student can become considerably aware of the pitfalls even without authoritative answers. This isn’t a particularly impressive brain dump file compared to the SAT recreations I’ve written about. But of course, the reddit thread where I found the google doc contained links to the several of the reading passages directly, and another thread openly discussed the specifics of a math problem. An employee or founder of Wave Tutoring was cheerfully in the same thread as the google doc link, giving advice and offering his services.

And there’s still good ol’ College Confidential, which has been the venue for organized SAT braindumping for years. The moderation appears a bit more vigilant this year, although the goal seems to be hiding evidence that cheating occurs rather than, you know, actually ending cheating.

So this page is blank because the moderator purged it, but the cache shows detailed question recollection. (Image capture in case cache disappears.) When a poster expresses surprise that there isn’t more specific chatter, he or she is told that just minutes earlier three pages of comments had been wiped out, presumably because students had been actively and specifically discussing the test.

I wonder if the reporters would have written cheerful stories about the google docs, the reading questions and topics, and the carefully worked math problems. Well. Not really. What I really wonder about is why the reporters can’t be bothered to write about the google docs, the reading topics, and the carefully worked math problems.

In the meantime, you can see why it’s all worth a chuckle. All this effort: the google files, the Tumbler memes, the careful hints, the chuckles, the sly media approval, and all this time the entire test was available online—and, undoubtedly, in hard copy for the right price.

Another College Confidential thread on SAT cheating via the forum inquires of the moderators why they allow blatant discussion of SAT questions without banning and posting a list of the offenders. A moderator responded that they have created a friendly place and that “public shaming” is not productive.

The discussion continues on to debate whether the site should be shut down so that the 10/28 PSAT isn’t compromised by all the “specific questions” being discussed.

What, you didn’t know that the PSAT isn’t over for the year? October 28, this Wednesday. Many high schools districts across the country take the PSAT on the “alternate date”: North Colonie Central Schools, Greenville High School, West High School, Dos Pueblos High School, Ridgefield High School, and the entire Seattle Public School District.

Is it the same test? Probably. I’m pretty sure the College Board used the same test for the “alternate” test date (note the wording) in the past. This year, with a new format, an entirely different test is probably impossible.

Wouldn’t it be cool if someone asked the College Board about it? Maybe a reporter, even.

Hey, David Coleman! Has your company discussed the publication of actual test material at College Confidential? The ACT constantly monitors the College Confidential boards for mention of their tests, but your company doesn’t. That’s why people routinely post passages and answers to SAT tests for the Chinese and Koreans too poor to pay for the actual tests from organized Chinese crime rings, while the ACT has almost no international market. But you don’t care about market advantage, right? You’re “non-profit”. In the future, are you planning on using previously issued tests for the international market, so the Chinese and Koreans can buy copies of the tests and pretend they are capable of 800 SAT reading scores when in fact they can’t even read English?

And speaking of the the Chinese SAT cheating ring, are your employees selling the tests? Maybe they’ve decided to develop a sideline in PSAT tests for Americans? Or perhaps the source is just a corrupt principal who sold a few copies to a test prep company and well, kids talk. But given the huge dollars schools pay for your product, have you considered delivering and proctoring the tests with College Board employees?

Do you have a different test planned for 10/28? If so, how will you ensure that the two different test dates are equally reliable?

If not, do you think it’s fair that all 10/28 PSAT testers, as well as 10/14 testers who had an actual copy of the test are better prepared to compete for the National Merit Scholarship Program, winning recognition and scholarships?

And please, Dave, don’t try and fob off questions with “Only a few schools take the test on the alternate date” or “The College Board spends millions on test security but we can’t be responsible for corrupt high school principals” or “We rely on our students’ honor and integrity and while there are sadly a few bad apples, the majority of our testers act responsibly”.

This is your product! You sell it to schools in exchange for a metric ton of money and student information–which you then turn around and sell to colleges, along with….oh, yeah, the TEST SCORES from a test that was available online for two weeks before the first sitting.

You’re busy breaking your arm patting yourself on the back for paying Khan Academy to provide low cost test prep to disadvantaged blacks and Hispanics—because you’re basically ignorant of the fact that blacks and Hispanics are more likely to get test prep than whites (all races are pikers compared to East Asians). Given your products’ abysmal integrity, why shouldn’t blacks and Hispanics abandon test prep and get in on the advance knowledge action? Right now, it’s probably (but not certainly) restricted to Asians, but that will change if you continue to shrug off the blatant test corruption that happens every month, every year–corruption that the ACT does not have in anything approaching the same level.

And while I’m on the topic, hey, Tim McGuire, president of the National Merit Scholarship Corporation! Have you ensured that PSAT is issued fairly and consistently, giving all testers an even shot at the scholarships you offer? Or are you so worried about constantly losing colleges that you ignore the fact that the PSAT is becoming as corrupt as its parent? Have you considered perhaps using an ACT product for scholarships?

Tish tosh, you say. No one really cares about the PSAT. It’s just a “practice” preliminary test. The scores don’t matter. They aren’t used for college admissions. So what’s the difference?

Yeah, you’re right. I shouldn’t point out that the kids most likely to use the advance copies are the kids who have a shot at National Merit scholarships. I shouldn’t remind everyone that the braindumping for the SAT, another College Board product, is exponentially worse than the violations I’ve discussed here. I shouldn’t worry that we’re becoming as corrupt as China. I shouldn’t worry that taxpayers pay millions to the College Board, a non-profit company, to deliver a testing product whose validity and reliability can’t be assured. I shouldn’t care that reporters don’t care enough to worry the College Board enough to bother scaring College Confidential, that reporters, like the colleges dropping the National Merit Program, only care about the average performance by SES and race.

What I really worry about, frankly, is all the organized braindumpers thinking jesus, that Ed. What a dolt. Only losers use College Confidential. You can download advance copies of all College Board products at darknet/yangchan for a small fee.

The Prima Donna Rock Star Tester Treatment

I met with her the first time last Sunday a week before the SAT, mother looking on, and the conversation went something like this.

“I want to specialize in one test. Which one should I take?”

“Yeah, okay, back up a bit. You took SAT test prep over the summer, right?”

“Yeah, but I knew everything they told me. It didn’t help.”

“What’s your course load?” (she goes to a 50% Asian school.)

” I’m taking a history honors class now, but it’s my first. Precalc for math.”

“And your GPA? What colleges are you considering? ”

Shrug. “3.8 or so. Colleges, I have no idea. But what I want to know is, should I specialize in the ACT or the SAT? And should I take the old one or the new one?”

“Do you have a target SAT score?”

“2000. What’s the equivalent in ACT? But I really think I should take the old SAT and be done. ”

“Your last practice test was a 1400.” She winced. “Even if all colleges take the old SAT for 2016 admissions–something I find unlikely despite assurances to the contrary–I’m not sure how you can find the time to focus on improvement between now and January, the last sitting of the old test. Besides, why the hurry?”

She waved dismissively. “I want to be done with all this. I hate the SAT. Maybe I should specialize in the ACT. I don’t want to learn the new SAT.”

“Yeah, we’re back to this whole ‘pick a test’ thing. Let’s discuss something touchier. Are you frustrated by the difference between your school performance and your test performance?”

She got very still. “Yes.”

“When I see an academic profile significantly higher than a test score, the student usually mentions it first. I’ve met many kids, a lot of them girls, with a profile like yours. They’ll tell me that they really just want to improve, to get their score into a respectable range, and that they haven’t had good luck with test prep so far. I didn’t hear any of that from you. Instead it’s ‘gotta pick a test’, need a 2000′ despite no college plans, without any acknowledgment of what must be a very disappointing practice history.”

I said all this as delicately as possible, but she was already surreptitiously wiping away tears.

” I don’t see your mom behind this. You’re causing your own pressure but are also very resistant to making more effort or exploring options.”

She started nodding before I finished, and her mom handed her a Kleenex. “I just think I’m wasting my time.”

“So let’s start there. Do you have trouble with school tests? No? How about your state tests? So it’s not a general testing problem, just big standardized tests. Is it nerves?”

She laughed, sadly. “No. My big problem is motivation.”

I snorfed involuntarily, and she looked up in shock. “Sorry. I’m not at all laughing at you. Just the idea that the kid I see in front of me barking orders like an executive suffers from motivation problems.”

The mother demurred here. “Well, her GPA is only a 3.8.”

“Forgive me, but you’re Chinese and prone to distortion on this point.” They’re American enough to laugh. ” I see an articulate, bright, driven girl who appears to have an intellect that I would put conservatively three or four hundred points above this practice score. You are using that intellect in school. I don’t see an obvious motivation issue.”

“No, not in school. Not studying. When I’m testing–you know, like the practice tests? I lose all motivation.”

Well, hey now.

“Tell me if any of this is familiar: The test begins and you’re working away, feeling good. Then you run into a problem that you don’t know how to solve and suddenly, as you try to figure the problem out, everything seems pointless. You give up, make a guess, go on to the next problem. Except now you aren’t sure what to do with this one, either. Suddenly, nothing matters. You simply stop caring. I see by your face that I’m not off-base.”

“How did you know?”

“I’ve seen it before. I describe it as a sort of stress reaction.¹”

” I’m not nervous at all.”

” You should be so lucky. Jitters don’t usually affect performance. You get bored by stress. What happens, best I can tell after hearing many students describe the feeling, is that your brain shuts down to avoid feeling stress.”

My first case was a short, slight blond boy back before the SAT changes, so before 2005. I was going through his practice test explaining the missed problems, and he’d finish my sentences. That is, he knew how to do many of the problems he’d gotten incorrect on the test.

So why the high error count, I asked.

It was after I got bored, he replied. Once the boredom hit, he’d start to randomly bubble. I was aghast. He may as well have told me he sucked dead chickens’ eyeballs for candy, so incomprehensible was his behavior.

“So what you have to start doing, have to understand, is that you are a testing prima donna.”

“A prima donna?”

“You know how movie stars always order off-menu? Because they’re just too special for the pre-arranged menu that the rest of us use. Or the ballerinas or opera stars who simply refuse to be rushed, because they are artists. Or rock stars, the kind who make huge demands for their hotel rooms sometimes—Van Halen famously demanded brown M&Ms be removed from the candy bowl (yes, I know they had another reason, but her parents are never going to let her listen to Van Halen, so I’m safe). You need to be a prima donna rock star tester.”

“How?”

“Take two SAT sections daily, from the blue book. Use deadly serious test conditions. No music. No interruptions. No stopping the clock. No laying on the floor or on your bed. Sit at a table, door shut, start the timer.”

“That’s not even an hour.”

“And when the timer starts, I want you to take two minutes, at least, to go through the test and cherrypick. Circle the problems you’ll deign to do.”

“Um. What?”

“In math, pick and choose your problems. Circle the good ones. ‘This one, I shall do. This one, pah!’ Spit upon it. If you don’t instantly vibe to the question, avert your eyes and scratch an X next to that problem, which clearly must be for peasants and other little people. Can you do that?”

She giggled. “Really? What about reading?”

” Skip anything with long paragraphs that looks less desirable than root canal. You like sentence completions?”

“Yes!”

“Do them first, then evaluate each reading passage to determine whether or not Her Majesty–that’s you–is interested. Which part of the writing section do you like best, the paragraph at the end?”

“How do you know this?”

“Do those six questions at the end first. Then go back to the front. The second–I mean the second—you find a long sentence you can’t instantly decipher, that question OFFENDS you. Turn up your nose. Move on.”

“So that’s all I want for the week. Two sections. Vary the subject. Every night. Take them like a rock star looking at candy bowls to make sure there are no…oh, look there’s a brown M&M. Skip it.”

“But I might only want to do four or five questions a section.”

“Great. Do those. Then, oh, hey. You’ve still got 20 minutes to kill. What’ll help pass the time? Let’s look at the other questions to see if they hold any interest. You are a movie star stuck in Podunk, in search of decent dim sum.”

“But the whole thing is a lie. The problems I can’t do aren’t stupid.”

“Sure, but we need to fake out your psyche. You have a fragile testing temperament that must be coddled and swathed in protective coating.”

The mom was a bit stunned, but accepting. “So none of the strategies she learned in test prep?”

“Mom, they didn’t work anyway. But what if I don’t have enough time to go back and do the problems that bored me?”

“Then you will have spent a whole test section working on problems you can do. How is that worse?”

“But if I try to read the long passages, I know I will get bored.”

“Well, I have some ideas for that later, but for now, read the passages that meet with your approval, and do the questions. Then for the rest, amuse yourself with the peasant passages. Do the vocabulary questions. The ones with line numbers. Don’t read them if they bore you. Normally, you understand, I wouldn’t suggest this.”

“So practice that all week. Eat pizza, chocolate, noodles, sesame balls with red bean paste, whatever your favorite food is Friday night. Saturday, have a good breakfast and visualize rejecting all those peasant problems.”

“What if I get bored anyway?”

“That’s a very real possibility. At the first moment you identify boredom, put your pencil down. Take a breath. Remind yourself that while it’s scary, this boredom is a valuable opportunity to practice dealing with it. That it only feels like boredom. Do not give up. Do not let yourself randomly bubble. If you feel done and can’t fight off the boredom, put your head down and take a nap. Otherwise, go back to the test and look for test questions that pique your curiosity.”

“But you said I didn’t have to read the passages.”

“Sure. But don’t randomly bubble, or give up. Estimate. Eliminate known wrong answers. Guess based on the context. But if you can’t kick off the boredom and feel hopeless, take a rest until the next section.”

“And here’s the important part: under no conditions are you to worry about your score. You’re not there for the score. You’re there to practice being a rock star who picks and chooses her projects. We’ll do scores later, if you like.”

“That’s okay. I don’t think I’m going to improve now, so at least I might know why.”

“It’s helpful just to know what the problem is,” her mother agreed.

They actually smiled as I left, both noticeably less anxious than they were when I arrived.

Note: she’s a junior, and has no reason whatsoever to take the SAT in October. I tried to talk the mom out of that, but she was determined to keep the date. Ideally, I wouldn’t send a student to try out this method on a live test, but that was the only option.

Will it work, this refusal to tolerate brown M&Ms and uninviting questions? Typically, yes, although since I’ve cut back on tutoring I haven’t run into the prima donna tester in several years. The cases I remember always saw an instant boost of 100-150 points the first time they took the test in rock star mode. In every case, they were also mentally exhausted afterwards. They’d never worked the entire test before, having mentally checked out. Prima donnas are fixable. The ones who go into a fugue state, not so much. Fortunately, that’s even rarer.

I started to make a larger point, but it’s too complicated and, since returning this August I’ve vowed to post more. I had too many ideas piling up that just weren’t…perfect, and so I kept putting them off, even though each idea had more than enough for a post. Time for me to limit scope and bite off achievable chunks. Otherwise I’ll think I’m bored and don’t care when really I’m stressed out….hey. Good thing I don’t get like this for tests.

So don’t read too much into this beyond an interesting behavior that I’ve learned to treat. Don’t apply it to policy. Do I think some people underperform their abilities on tests? Yes, I do. Do I think that tests can be gamed by people whose essential intelligence is high on mimicry and memory, giving the impression of skills they don’t actually have? Yes, I do. Do I think tests are mostly accurate? Yes, for most people. It’s a big ol’ world out there. Many cases exist simultaneously.

Meanwhile, I hope all you testers out there did well yesterday. And if you know any fragile testing temperaments, give this strategy a try.

**********************************
¹ While writing this piece, I googled and learned that researchers call it stress, too.