The Sum of a Parabola and a Line

For the past two years, my algebra students have determined that the product of two lines is a parabola, which instantly provides a visual of the solutions and the line of symmetry.  For the past year, they’ve determined that squaring a line is likewise a parabola, and can be moved up and down the line of symmetry, which is instantly visible as the line’s x-intercept. In this way, I have been able to build understanding from lines to quadratics without just saying hey, presto! here’s a parabola. I introduce them to adding and subtracting functions, and from there, it’s a reasonable step to multiplying functions.

Typically, I’ve moved from this to binomial multiplication, introducing the third form of the quadratic we deal with in early high-level math, the standard form. (The otherwise estimable Stewart refers to the vertex form as standard form, to which I say sir! you must reconsider, except, well, he’s dead.)

At some point in teaching this, you come to the “- b over 2a” (^-b⁄_2a) issue. That is, teachers who like to build on existing knowledge towards each new step are a bit stuck when it comes to finding the vertex in a standard form equation.

(For non-mathies, the standard form of an equation is ax²+bx+c and the vertex form is a(x-h)²+k.  The parameters “a” “b”, and “c” are often just referred to by letter. Vertex form, we’re more likely to talk about the x and y values of the vertex, just like  when we talk about lines in the form y=mx+b, we don’t say “m” and “b” but rather “slope” and “y-intercept”. But teachers, at least, often talk about teaching different aspects of standard form operations by parameters: a>1, a<0, to say nothing of the quadratic formula.  So the way to find the vertex of a parabola in standard form is to take the “a” and “b” term and use the algorithm ^-b⁄_2a to find the line of symmetry,  which is the x-value of the vertex. Then”plug it in”, or evaluate, the x-value in the quadratic equation to find the y-value for the vertex.)

The only way I’ve found until now of building on existing knowledge to establish it is setting standard form equal to vertex form to establish that the “h” of vertex form is equal to the ^-b⁄_2a of standard form, something only the top kids really understand and don’t often enjoy. (they’re much more interested by pre-calc.)

Last year, I was putting together a worksheet on adding and subtracting lines, and on impulse I added a few that involved adding a simple parabola with its vertex at the origin with a line, mainly to add a bit of challenge for the top kids. I could see that adding a line and a parabola doesn’t provide the instant visual “hook” that multiplying or squaring lines does.

It’s obvious that the y-intercept of the sum will be the same as the y-intercept of the line. One can logically ascertain that in this particular case, the right side of the y-axis will only increase—adding two positives. The left side, therefore, as x approaches negative infinity is where the action is. But not too much action, since the parabola’s y is galloping towards positive infinity at a faster clip than the line’s is trotting towards negative infinity. So for a brief interval, the negative of the line will offset a bit of the positive of the parabola, but eventually the parabola’s growth will drown out the line’s decline.

All logically there to construe, but far less obvious at a glance.

This year, I decided to explore the relationship further, because deciphering standard form is where my weakest kids tend to check out. They’ve held on through binomial multiplication, to hang on, at least temporarily, to the linear term so that (x+3)² doesn’t become x² + 9. They’ve mastered factoring quadratics, to their shock. They understand how to graph parabolas in two forms. And suddenly this bizarre algorithm that has to be remembered, then calculated, then more calculations to find “y”, whatever that is. Can you say “cognitive load“, boys and girls? Before you know it, they’re using the quadratic formula for linear equations and other bad, bad things that happen when it’s all kerfluzzled in their noggins. That’s when you realize that paralysis isn’t the worst thing that can happen.

Could I break the process down into discrete steps that told a story?  Build on this notion of modifying the parent function ax² with a line to shift it left or right? Find Raylene a new kidney now that her third husband discovered her affair with the yoga instructor and will no longer give her one of his?

My  first thought was to wonder if the slope of the line had any relationship to the graph’s location. My second thought was yes, you dweeb, “b” is the slope of the added line and b’s fingerprints are all over the line of symmetry. No, no, the other half of my brain, the English major, protested. I know that. But is there some way I can get the kids to think of “b” as a slope, or to link slope to the process in a meaningful way?

(This next part is probably incredibly obvious to actual mathematicians, but in my own defense I ran it by three teachers who actually studied advanced math, and they were like hey, wow. I didn’t know that.)

What information does standard form give? The y-intercept, or “c”. What information do we want that it doesn’t readily provide? The vertex. Factors would be nice, but they aren’t guaranteed. I always want the vertex. So if I graph the resulting parabola of the sum of, say,  x² and 6x + 5, how might the slope be relevant?

The obvious relationship to wonder about first is the slope between the y-intercept, which I have, and the vertex, which I want. Start by finding the slope between these two points. And right at that point I realize hey,  by golly, that’s the rate of change(!).

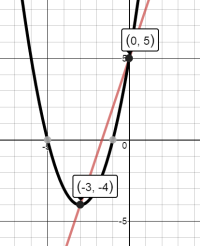
The slope–that is, by golly, the rate of change(!)–is 3. The line of symmetry is -3. The vertex is exactly 9 units below the y-intercept, or the product of the rate of change and the line of symmetry. Heavens. That’s interesting. Does it always happen? Let’s assume for now a=1.

Sum	Slope from y-int to vertex	Line of Symmetry	units from y-int to y-value of vertex	Vertex
x2 – 4x – 12	-2	x=2	-4	(2,-16)
x2 – 10x + 9	-5	x=5	-25	(5,-16)
x2 – 2x – 3	-1	x=1	-1	(-1,-4)
x2 +6x + 8	3	x=-3	-9	(-3,-1)

Hmm. So according to this, if I were trying to get the vertex for x² +12x + 15, then I should assume that the slope–that is, by golly, the rate of change(!)– from the vertex to the y-intercept is 6. That would make the line of symmetry is x=-6. The y-value of the vertex should be 36 units down from 15, or -21. So the vertex should be at (-6,-21). And indeed it is. How about that?

So what happens if a is some other value than 1? I know the line of symmetry will change, of course, but what about the slope–that is, by golly, the rate of change(!). Is it affected by changes in a?

Sum	Slope from y-int to vertex	Line of Symmetry	units from y-int to y-value of vertex	Vertex
2x2 – 8x – 5	-4	x=2 (-4/2)	-8	(2,-3)
-x2 +2x + 4	1	x=1 (-1/-1)	1	(1,5)
-2x2 +14x +7	7	x=3.5 (-7/-2)	24.5 (49/2)	(3.5,31.5)
4x2 +8x -15	4	x=-1 (-4/4)	-4	(-1,-19)

Here’s a Desmos application that I created to demonstrate it.  The slope–that is, by golly, the rate of change(!)–from the vertex to the y-intercept is always half of the slope of the line added to the parabola–that is, half of “b”. The rate of change is not affected by the stretch factor, or a. The line of symmetry, however, is affected by the stretch, which makes sense once you realize that what we’re really calculating is the horizontal distance (the run) from the vertex to the y-axis. The stretch would affect how quickly the vertex is reached. So the vertex y-value is always going to be the rise for the number of iterations the run went through to get from the y-axis to the line of symmetry, or the rate of change multiplied by the line of symmetry x-value.

Mathematically, these are the exact steps used to complete the square but considerably less abstract. You’re finding the “run” to the line of symmetry and the “rise” up or down to the vertex.

Up to now, I’ve been describing my own discovery? How to explain this to the kids? As is always the case in a new lesson, I keep it pretty flexible and don’t overplan. I created a quick activity sheet.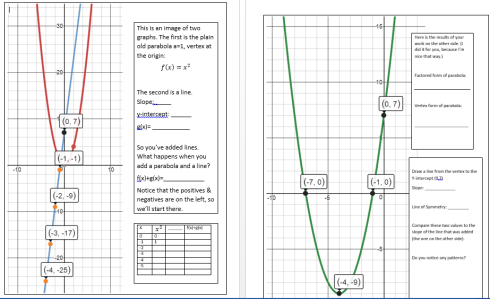

The goal here was just to get things started. Notice the last question on the back: “Do you notice any patterns?” I was fully prepared for the answer to be “No”, which is good, because it was. We then developed the table similar to the first one above, and they quickly caught on to the pattern when a=1.

I was a bit worried about moving to other a values. However,  the class eventually grasped the basic relationship. The slope from the vertex to the y-intercept was always related to the slope of the line added  to the parabola. But the line of symmetry, the distance from the y-axis, would be influenced by the stretch. This made intuitive sense to most of the kids. They certainly screwed up negatives now and again, but who doesn’t.

Good math thinking throughout. I heard a lot of discussions, saw graphs where kids were clearly thinking through the spatial relationship. Many kids realized that when a=1, a negative b means the slope of the line from the y-intercept to the vertex is also negative, which means the vertex must be to the right of the y-intercept. A positive “b” means the slope is positive which means the vertex is to the left. Then they realize that the sign of “a” will flip that relationship around. he students start to see the “b” value as an indicator. That is, by making bx+c its own unit, they realize how important the slope of the added line is, and how essential it is to the end result.

All that and, you might have noticed, they get an early peek at rate of change concepts.

Definitely no worse than my usual ^-b⁄_2a  lesson and the weak kids did much, much better. This was just the first run; the next time I teach algebra 2 I’ll get more ambitious.

So I can now build on students’ existing knowledge to decipher and graph a standard form equation rather than just provide an algorithm or go through the algebra. On the other hand, the last tether holding my quadratics unit to the earth of typical algebra 2 practice has been severed; it’s now wandering around in the stratosphere.

I don’t mean the basics aren’t covered. I teach binomial multiplication, factoring, projectile motion, the quadratic formula, complex numbers, and so on. But the framework differs considerably from my colleagues’.

But if anyone is thinking that I’m dumbing this down, recall that my students are learning that functions can be combined, added, subtracted, multiplied. They’re learning that rate of change is linked directly to the slope of the line added to  the parabola, and that the original parabola’s stretch doesn’t influence the rate of change–but does impact the line of symmetry. And the weaker kids aren’t getting lost in algorithms that have no meaning.

I could argue about this, but maybe another day. For now, I’m interested in what to call this method, and who else is using it.