What I Learned: Year 3

I want to continue my teaching retrospective, if only for my own edification. Year 3 in particular led to major changes in my curriculum and pacing.

To recap: my first year was spent in a very progressive school, where I taught algebra, geometry, and humanities, both literature and history. I loved teaching, didn’t much care for the school, and definitely wasn’t sufficiently of the left to stay there. Years 2 and 3 were at a Title I school, 65% Hispanic/ELL. As I’ve said before, year 2’s all algebra all the time schedule was my toughest schedule ever as a teacher; I do not expect to see its like again. Which is good, because I still get flashbacks. I have, in fact, never officially taught algebra 1 since that time although most people would consider what I teach in Algebra 2 to be, in fact, Algebra 1.

Year 3 was at the same school, but I was assigned Algebra 2 and Geometry. And that made all the difference.

Establishing Classroom Ambiance

My 65 geometry students included twenty I’d taught the previous year in Algebra I, students who knew and liked me.

First day, I started one class a bit early when in walked Robbie, redheaded, pale, anxious, diagnosed with Asperger’s but almost certainly a high functioning autistic. I told him to have a seat, and didn’t immediately realize that the little freshman was utterly aghast at the idea that he was late to class. He was murmuring “class starts at 9:15, I was here at 9:12” over and over again, slowly working up to a meltdown by the time I noticed. Before I could react Augustin, a junior, first student I’d met at this school the year before, leaned over from a desk in the same group.

“Relax. Teacher started early. Never cares about time anyway. You’re good.”

Meltdown over. Robbie was awestruck that a junior had deigned to notice him. He also remembered all year that I “never cared about time”, which did much to keep him balanced and happy with a teacher incapable of a predictable routine. I have always remembered Augustin for his offhand kindness to an odd kid.

My geometry classes gave me the feeling of being a known quantity, a teacher with student cred, something I’d long easily established in my Asian enrichment classes, as well as my Kaplan test prep, but never felt in a public school before. I’d always been a loose disciplinarian, an easy classroom controller, and this isn’t as easy in test prep as you might think—it’s why I got so much work. I knew that teaching outside of private instruction would be different, but I found the change more challenging than I expected.

For my first two years in public school, I struggled to recreate the friendly “we’re all in this together” atmosphere I expected to achieve easily. My first year, only my humanities class ever achieved the ambiance I took for granted in private instruction. Only two of my 4 algebra classes (one was a double block) had that cheerful noisiness that is now a trademark of my public school classes. I wasn’t a failure as a teacher; in many ways, I was doing exactly what I anticipated and dealing with expected obstacles. But I had secretly mourned the loss of my standing as a popular teacher. And now, suddenly, I had my mojo again.

My algebra 2 classes were more like my algebra 1 classes from the year before; I didn’t have yet the same easy rapport that I had with my geometry students. This gave me a chance to study the difference. Would I always need to have repeat students, or was there something I could do to establish the environment of easy fun with hard work–or at least some effort?

Over time, I learned that some students find me harder to understand than others. They often don’t grok my ironic asides. They do not understand that I “blast” without malice. They assume I hold grudges, that I count misdemeanors in a black book somewhere. They don’t understand I am often somewhat ruthlessly focused on one objective. As I’ve said before, teaching is a performance art, and the act of engaging students to convince them to learn is often an arduous mental task.

And so I’ve learned to explain this up front. That I am often sarcastic, and think attempts to ban this essential classroom management tool are Against God. That I’m not often annoyed, and usually harmless. But when I am annoyed I yell first, ask questions later when I remember to, which I often don’t. That I am unlikely to remember what I was mad about 20 minutes later, much less hold a grudge. In fact, the only behaviors that I remember are cruelty and cheating. That I love teaching, and like all of them. Except Joe. I can’t stand Joe. And frankly, I’ve never been a big fan of Alison. But except them. And Mario. Don’t care for Mario much. But everyone else. Really. (Yeah, see that, kids? Mild irony. Get used to it.)

I’ve also learned to reach out on things that don’t matter as much to me but I’ve realized matter much more than I realized to students. I’ve always been one to say “Hi!” in the hallways and chitchat for a moment with past and present students but in truth honestly don’t care about football games or sporting events. Still, kids really do like it when you show up at the games, or ask about the outcomes, or call out a student who had a great game or ran a PR. I ban the singing of Happy Birthday because the noise is unbearable, but after they beg, I give them a count of three and we all shout the phrase at once. And all my classes delight in realizing how easy it is to drive me off-topic by asking about food or politics.

All my ability to deliberately set a classroom environment came from the lucky break of teaching geometry to some of the same students I’d just passed in algebra.

Coverage vs. Comprehension

I sure hope Bud Blake got credit for this 1974 classic, reproduced daily in ed school and professional development lessons everywhere.

I used to take state tests more seriously, and was quite proud that my first year out, I “hit the dinger” in geometry and algebra. I hadn’t rushed, and even back then had deemed many topics non-essential, or at least far less important than others. My students were doing reasonably well on tests, which were free-response that year.

But towards the end of the year, I realized with a shock that many of my mid-tier students had forgotten most of the content. Students who understood the Pythagorean Theorem were now marking up triangles with SOHCAHTOA when they had two sides and just needed the third. Algebra students were plugging linear equations into the quadratic formula. Cats were sleeping with dogs. All was not right. It was as if they’d never been taught.

Year two, I was primed to look for learning loss but pacing was so impossible with the wide ability range that I instituted four levels of differentiation. I succeeded in slowing down instruction and letting students absorb more information.

But year three saw my first attempts to help Stripe learn to whistle.

In geometry, the first sign of change came in October. I’d explained transversals of parallel lines. I’d done a great job. Brilliant, even. Not content to simply lecture, I asked questions, prompted discussion, ensured students saw the connection and sketched the familiar representation.

And the lesson didn’t thud. All the students obediently worked the problem set. They asked reasonable questions.

So I don’t know, really, what compelled me to double check.

“Am I picking up a weird vibe? You all are working, but I have this sense that you’re still confused.”

Murmurs of agreement.

“How about everyone close their eyes and we’ll do a thumb check?” (I rarely use such obvious CFUs these days, but they’re still a great tool for uncertain situations.)

Most of the thumbs came up sideways.

So I told the kids I’d think about this for a while, and came back with an activity, one that required about $70 in materials that I still use to this day.

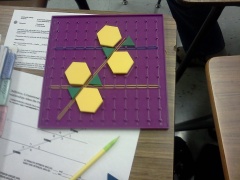It worked. The transversal angle relationships were easier to understand with the physical representation, the students could see the inevitability, see how the angles “fit”. And from that point, they could easily see that unless the transversal was perpendicular, each transversal over parallel lines formed only two distinct angle measurements: an obtuse and an acute.

A nifty transversal lesson wasn’t the important development, even though my geometry students still enjoy the activity almost as much as they enjoy creating madcap patterns with the boards and rubber bands.

Sensing confusion despite a generally successful lesson, I had developed an illustration on my own to develop a stronger understanding. I was beginning to spot the difference between teaching and learning.

I still struggle with this. It’s very easy to get sloppy, particularly in a large class with ability ranges of 4 to 5 years, with kids in the lower ranges happily sleeping through classes, stirring themselves only enough to beg me for a passing grade. But ultimately, I circle back with yet one more pass through, coming up with an illustration or series of problems to shine a light on confusion.

I’ve written extensively of Year 3’s other major development. Faced with the reality that I’d wasted a semester covering linear equations and quadratics that students didn’t remember in the slightest, I decided to start over, beginning with modeling linear equations. Not only did I completely change my approach to curriculum, I also flatly punted on coverage from that point on, focusing on the big five for every subject. As I improve at introducing and explaining concepts, my students become capable of taking on more challenging topics; the interaction between my curriculum and student understanding is very much a positive feedback loop.

Ironically, my decision to abandon coverage was driven in part because Algebra 2 was a terminal course, meaning it was to be offered only to remedial seniors, students were not expected or in fact allowed to take any other math course. For this reason, I felt free to craft my own course to focus purely on getting the students ready for college math. But at least half of my students were juniors, and most of them took pre-calc the next year. This was my first exposure to Algebra 2’s dual nature. More on that later.

Mentoring Colleagues

For my first two years, I had almost no contact with colleagues. Year 3, two new math teachers joined and we instantly hit it off. Went for coffee on late start mornings, beers after work. I was their resource; both of them found me far more helpful than their assigned mentors. I still meet up with both of them four or five times a year at least.

I left that year for my current school, and went over two years again without any real colleagues. I missed it. Having spent most of my professional life working without colleagues that liked lunch, beer, coffee, whatever, I can map out the exception eras, and treasure them. Last year I began mentoring, and now have lunch, coffee, whatever with them individually and together.

I’m not chummy enough, much less normal enough, to bond easily with other teachers. But I’m a good mentor, and that seems to be how I make friends as a teacher.

Finally, Year Three taught me how to cope with genuinely unfair treatment, which I haven’t often had to deal with. I never go into details about it, but while I wasn’t crazy about the school, I didn’t want to look for jobs again. Being a fifty year old teacher without a job is a Very Bad Thing—of course, take out the word “teacher” and it’s still true, probably more so.

On the other hand, while I wasn’t crazy about that school, I am very happy at this one. What do they call that, perspective?