Teaching Math a Third Way

I was reading Harry Webb’s advice to a new secondary teacher, describing his usual classroom procedure for “senior maths”, as an addendum to his earlier post on classroom management. And I thought hey, I could use this to fully demonstrate the difference in math instruction philosophies.

Harry’s lesson is a starting activity, a classroom discussion/lecture, and classwork.

So here’s what I did on Friday for a trig class, which is certainly “senior maths”: brief classroom discussion, class activity (what Harry would call “group work”), brief classroom discussion. And I think it’s worth showing that difference.

The kids walked in, sat in assigned seats grouped in fours—strong kids in back, weakest in front. I often forget and start before the tardy bell, just laying out what we’ll do that day. I never check homework—the kids take pictures and send it to me, and I eventually get it into the gradebook. I don’t really care if kids do homework or not. They take pictures of it and text or email me. I eventually check. If kids have homework questions, they’re to let me know during the tardy pause and I’ll review them on an as-needed basis. But yesterday, the kids hadn’t had homework, so not an issue.

When the tardy bell rang, I had just finished sketching this:

(this next bit is what I think Harry would call classroom discussion):

“Can anyone tell me the relationship these triangles have?”

I got a good, solid chorus of “similar” from the room—not everyone, but more than a smattering. I picked on Patti, up front, and asked her to explain her answer.

“They have two congruent angles.”

“Good. Dennis, why do I only need to know about two of the angles?”

Dennis did the wait out game, but I’m better. After a while, he said, “I don’t know.”

“Do you know how many degrees are in a triangle?”

“180. Oh. OK. If they add up to 180, and two of them are equal, the third one has to be the same amount to get to 180.”

“See, you did know. Jeb, if two triangles are similar, what else do I know?”

Jeb, in the back corner, said “The sides have a constant ratio.”

“More completely, the corresponding sides of the triangle have a constant ratio. Good. How many people remember this from geometry?” All the hands are up. “If you had me for geometry, and about eight of you did, you may even remember me saying that in high school math, similarity is much more important than congruence, for high school math, anyway. Trigonometry will prove me right once again. So while I hand out the activity, everyone work the problem.”

When I got back up front, I confirmed everyone knew how to solve that, then I went on to this:

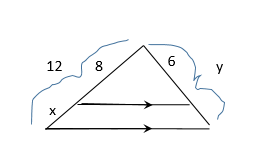
“I don’t want everyone to answer right away, okay? I’ll call on someone. Give people a chance to think. Which one of these variables can be solved without a proportion? Olin?”

Olin, very cautiously: “x?”

“Because…”

“I can just…see what I add to 8 to get 12?”

“Right. Now, that probably seems painfully obvious, but I want to emphasize—always look at the sketch to see what you know. Don’t assume all variables take some massive equation and brain work. Now, how can I find the length of the other side? Alex?”

“I’m just trying to figure that out.”

“You’re assuming the triangles are similar? Can she do that, Jamie?”

“Yes, because the lines are parallel.”

“Hey, great. Why does that help, Mickey?”

“I don’t know.”

“Cast your mind back to geometry. Which you took with me, Mickey, so don’t make me look bad. What did we know about parallel lines and transversals?”

“Oh. Oh, okay. Yeah. the left angles are congruent to each other, and the right ones, too.”

“Because….”

“Corresponding angles,” said Andy. I marked them in.

“Okay. So back to Alex. Got an equation yet?”

“I don’t know what I should match with what.”

“Okay. So this, guys, is the challenge of proportions. What will give me the common ratio that Jeb mentioned? I need a valid relationship. It can be two parts of the same shape, or corresponding parts from different shapes. Valicia?”

“Can I match up 8 and 6?”

“Can she?”

“Yes,” said Ali. “They are corresponding. But we don’t know what the short leg is.”

“We don’t need to,” says Patti. “6 over 8 is equal to y over 12.”

After finishing up on that problem, I turned to the handout.

“I stole this group of common similar triangle configurations, just as a way to remember when they might show up. But we’re going to focus on the sixth configuration. Can anyone tell me what’s distinctive about it?”

“It’s a right triangle with an altitude drawn,” offered Hank.

“True. Anything unusual?”

“No. All triangles have altitudes.” He looked momentarily doubtful. “Don’t they?”

“They do. So take a look at this” and I draw a right triangle in “upright” position. “Where do I draw an altitude?”

“You don’t need to….Oh!” I hear talking from all points in the room, and pick someone up front. “Oscar?”

“That’s the altitude,” he points. I wait. “The—not the hypotenuse.”

“Melissa? Can you give me a pattern?”

Melissa, in back, quite bright but never volunteers. “If the leg is a base, then a leg is the altitude.”

“True for all triangles?”

“No. Just for rights. Because the legs are perpendicular.”

“Right. So back to Oscar, what’s different about this?”

“The hypotenuse is the base.”

“Right. So it turns out that the altitude to the hypotenuse of a right triangle is….interesting. Turn over the handout.”

The above conversation, which takes a while to write out, took about 15 minutes, give or take. I would expect Harry Webb has similar stories.

The next part of my lesson is the “group work” that Harry and other traditionalist think leads to “social loafing” and wasted time.

The kids are in ability groups of four; they go to whiteboards spaced all around the room: two 5X10s, 3 4x4s, and self-stick on bulletin boards that works great—I even have graphs attached.

And I just give them instructions and say, “Go.”

Is this discovery math? Hell, no. I give them all sorts of instructions. I don’t want open-ended exploration. What I want for them is to do for themselves and understand what I would have otherwise explained.

In the next 50 minutes, using my instructions, each group had identified the three triangles:

There’s always a surprise. In this case, more of the kids had trouble proving the similarity (that is, all angles were congruent) than with the geometric mean. I actually stopped the activity between steps 1 and 2 to ensure everyone understood that the altitude creates two acute angles congruent to the original two–which I frankly think is pretty awesome.

Even before they’d quite figured out the point of the angles, they’d gotten the ratios:

Each of the nine groups found the second step, proving the altitude (h) is the geometric mean of the segments (x & y) on their own; I confirmed with each group. Once they’d established that, I reminded them that the third step was to prove the Pythagorean theorem and to look for algebra that would get them there. Four of the groups had identified the essential ratios, identifying that a² = xc and b² = yc.

At that point, I brought it back “up front” and finished the proof, which requires three non-obvious steps.

a² + b² = xc + yc (reminding them about adding equations)

Then I waited a bit, because I wanted to see if the stronger kids pick up on the next step.

“Just think, a minute. Remember back in algebra II, when you were solving for inverses.”

“…Factor?” says Andy.

“Oh, I see it,” Melissa. “factor out the c.”

“Right. So then we have a² + b² = c(x+y)”

“Holy sh**.” from Mickey.

“Watch the language.”

“That is so cool.” says Ronnie, who is UP FRONT!

“if you don’t know what they’re saying, everyone, look at the diagram and tell me what x+y is equal to.”

And then there were a lot of “Holy sh*–crap” as the kids got it. Fun day.

I wrapped it up by reminding them that we were just doing some preliminary work getting warmed up to enter trig, but that they want to remember some key facts about the geometric mean, the altitude to the hypotenuse of a right triangle. Then I go into my spiel on the essential nature of triangles and we’re all done. Homework: Kuta Software worksheet on similar right triangles, just to give them some practice.

This lesson would rarely be included in a typical trig class, whether reform or traditional. I described the thinking that led to the sequence. But it’s a good example of what I do. (Also, as many bloggers have pointed out, my attention to detail is dismal, both in blogging about math and teaching it. Kids usually pick up on stuff I miss, and if it’s something big, I go back and cover it.)

I vary this up. Sometimes I go straight to an activity they do in groups (Negative 16s and Exponential Functions), other times I do a brief classroom discussion/lecture first (modeling linear equations and inequalities). Sometimes I have an all practice day or two—I’ve covered a lot of material, now it’s time to work problems and gain fluency (that’s when the tunes come out).

I originally had more but somehow the length got away from me, so I’ve chopped this down.

I have developed this method because I was never happy with traditional math, whether lecture or class discussion. The difference is not solely about the method of delivery; my method requires more time, and thus the pace is considerably slower.

The jury’s in on reform math: it doesn’t work well in the best of cases, and is devastatingly damaging to low ability kids. Paul Bruno refers to reform math as the pedagogy of privilege, and I agree. But it’s worth remembering that reform math evolved as a means of helping poor and black/Hispanic kids. Why? Because they weren’t interested in traditional math methods, and were failing in droves.

Ideally, we would stop forcing all kids into advanced math. But since that’s not an option, I think we need to do better than the carnage of high school math as we see it today: high failure rates, kids forced to repeat classes two or three times Given the ridiculous expectations, traditional math is due for some scrutiny, particularly in its ability to leave behind kids without the interest or high ability to carry them through. Let’s accept that most kids can’t really master advanced math. We can still do better. This is how I try for “better”.

I still have problems with students forgetting the material. I still teach kids who aren’t cognitively able to master higher level math. I’m not pretending the problems go away. But the students are willing to try. They don’t feel hopeless. They aren’t bored. I don’t often get the “what will we use this for” question—not because my math is more practical, but because the students aren’t looking for an argument. (And when they do give me the question, I tell them they won’t. Use it.) However, as I mentioned in the last post, I now have had students two or three years in a row. They were able to pass subsequent classes with different teachers, but they haven’t lost the ability to launch into an activity and work it, having faith that I’m not wasting their time. That tells me I’m not doing harm, anyway.

Math Instruction Philosophies: Instructivist and Constructivist

Harry Webb has been on a tear about discovery vs. traditional explanations. The hubbub has pulled the great god Grant Wiggins, originator of backward design, which is a bible of ed schools as a method for developing curriculum.

Now, let us pause, a brief segue, to reflect on those last two words. Developing curriculum. I’m talking about teachers, yes? Teachers, building their own unit lessons, their own tests, their own worksheets. As I’ve written, teachers develop their own curriculum and, to varying degrees, have intellectual property rights (I would argue) to their material. So when reformers, unions, politicians, or whoever stress the importance of curriculum, textbooks, and professional development in implementing Common Core, there’s a whole bunch of teachers nationwide snorfling at them.

So Wiggins and Jay McTighe wrote Understanding by Design, which describes their framework and approach to curriculum. It is, as I said, a bible of ed schools. I have a copy. It’s good, although you have to look past their irritating examples to figure that out.

(Note: See Grant Wiggins’ response below. I’ve reworded this slightly and separated it to respond to his concerns. Also throughout, I changed “direct instruction” to some other term, usually instructivism.)

The book clearly states that there’s no one correct approach for every situation, that arguing between instructivism and constructivism creates a false dichotomy. So I was jokingly sarcastic before, but my point is real: it’s hard to read Grant Wiggins and not think that, so far as K-12 curriculum goes, he leans heavily towards constructivist. As one example, in a text section that discusses the fact that there’s no one right approach, he includes this table on the activities dominant in each approach. When I look at this table, I see a clear preference for constructivist approaches. I also see it in this highly influential essay and much of his writing. But as Wiggins states in the comments, and in the book, he clearly denies this preference. However, Wiggins’ book is the bible of ed schools for a reason, and it’s not for its categoric embrace of all things instructivist. So put it this way: what he says are his preferences and what any instructivist would take away from his preferences are probably not the same thing. I say this as someone who periodically rereads his work because of the value I find in it once I shift my focus away from the trappings and focus in on the substance. I encourage anyone who agrees with my impression of Wiggins’ preference to read him closely, because he’s done a lot over time to inform my approach to curriculum development.

(end major edits–I put the original text at the bottom)

So Wiggins reads all this hooha, and comes out with this outstanding description of lectures and why they are a problem. I agreed with every word of this post (there are two others), so much so that I tweeted on it. (Note: I agree for math. History’s a different issue.) As I did so, I was vaguely disturbed, because look, while I don’t write a lot about ed school per se (and even defend it, slightly), I spent a lot of time in class naysaying. And if they’d been saying reasonable things like this about lectures, what had I been disagreeing about?

And then Harry comes through brilliantly, answering my question and pointing out a huge hole in Wiggins’ 3-part series:

Wiggins writes of a survey of teachers in order to support his view that different pedagogies are required to achieve different aims. Unsurprisingly, the teachers give the right answers; the ones that they probably learnt at Ed School. However, the survey response that is taken to represent lecturing is called, “DIRECT TEACHING Instruction on the knowledge and skills.” Now, although I do not recognise my practice in Wiggins’ definition of lecturing, I do recognise myself in this definition wholeheartedly. And so I think we are being invited here to see all direct teaching – dare I say direct instruction – as non-interactive lecturing that lasts for most of a period.

Hey. Yeah. That’s right! Wiggins naysays the lecture in his essay, but the overall debate is between instructivism, of which lectures are just a part, and it’s , and it’s instructivism that has a bad name in ed school, not solely lectures. Harry says that he explains in classroom discussion, but rarely lectures. Which may sound like someone else.

Harry scoots right by this, because he’s all obsessed about the fuzzy math and constructivist debate, and it occurred to me that this area needs elucidation, because most people—and reporters, I am looking at you—don’t understand this difference.

So here it is: not all explanation is lecture, and not all discovery is constructivist.

In an effort to not turn all my posts into massive tomes (don’t laugh), I’m going to write about this difference later. Here, I’m just going to show you the difference through different teachers.

Before I start: labels are hard. Roughly, the terms reform, student-centered, constructivist, “facilitative” (Grant Wiggins’ term) all refer to the open-ended investigative approach. Instructivist, teacher-centered, traditionalist, direct instruction are all terms used to describe the approach where the teacher either tells you how to do it or wants you to figure out the way (not a way) to do it. (Note: I left “direct instruction” in here, because I believe it’s still an instructivist approach.)

Very few math teachers are pure constructivist. We’re talking degrees. I have no data on usage rates, but I’d be pretty surprised if 80% of all high school math teachers didn’t use traditional instruction-based approach for 90% of their lessons. I speak to a lot of colleagues who dislike pure lecture and would like to teach a more modified instructivist mode, but they aren’t sure how it works. However, most high school math teachers are instructivists who lecture. Full stop.

Constructivist Approach (aka investigation, reform)

Dan Meyer: Dan Meyer’s 3-Act Meatballs
Fawn Nguyen: Barbie Bungee
Fawn Nguyen Vroom Vroom
Michael Pershan: Triangles and Angles (he calls this investigation. I’d personally characterize it as “in between”, but it’s his call.)
Cathy Humphries: Investigation into Quadrilaterals

This is a partial list. Dan’s blog has links to all his various projects, as well as other bloggers committed to the investigative approach.

(By the way, I am dying to do the Vroom Vroom one, but I’m not enough of a mathematician to understand the math behind it. Neither does Fawn, apparently. The math looks quadratic. Is it?)

I’m not a fan of the open-ended reform approach, but I like all sorts of the activities the constructivists come up with. I just modify them to be more instructivist.

Remember that both Meyer and Nguyen use worksheets, practice skills, and many other elements that are pure instructivist. Pershan rarely does open-ended activities. In contrast, Cathy Humphries is very close to pure constructivist math. Total commitment to reform.

Traditional Instructivism (Lectures)

Much MUCH harder to find traditionalists bloggers. I’ve included two of my “lectures” that have relatively little discussion, just to fill out the list:

Me: Geometry: Starting Off
Me: Binomial Multiplication and Factoring with the Rectangle

Dave at MathEquality is traditionalist, a guy who works hard to explain math conceptually, but does so for the most part in lecture form. However, it’s also clear he keeps the lectures fairly short and gives his students lots of in class time for work.

But he’s the only one I can find. Right on the Left Coast appears to be a traditionalist, but he writes more about policy and his disagreement with traditional union views. (Huh, I should have mentioned him in my teacher blogger writeup of a while back.)

In order to give the uninitiated a good idea of what lecture looks like, three google searches are informative:

factoring trinomials power point

holt math power point

McDougall Litell math power point

Many high school teachers build their own power point explanations. Others just take the ones provided by publishers.

Still others use a document camera or, if they’re extremely old-school, transparencies.

What they look like is mostly this:

Khan Academy: Isosceles Right Triangles

Many teachers are really, really irritated at the fuss over Khan Academy because all he does is lecture his explanations—and not very well at that.

The most vigorous voices for traditional direct instruction comes from people who don’t teach high school math. That’s not a dig, it’s just a fact.

Modified instructivist

I’m not sure what to call it. There’s not just one way to depart from instructivist or constructivist. The examples here generally fall into two categories: highly structured instructivist discovery, and classroom discussions with lots of student involvement.

Me:Modeling Linear Equations
Me: Modeling Exponential Growth/Decay
Michael Pershan: Proof with Little Kids
Michael Pershan: Introducing Polar Coordinates
Michael Pershan: The 10K Chart
Ben Orlin: …999…. and the Debate that Repeats Forever.
Ben Orlin: Permutations and combinations

For a complete list of my work, check out the encyclopedia page on teaching. I likewise recommend Pershan and Orlin’s blogs.

A question for Grant Wiggins, and anyone else interested: what differences do you see in these approaches?

A question for reporters: when you write about reform or traditional math, do you have a clear idea of what the fuss is about? And did these examples help?

Question for Harry Webb: You sucked me into this, dammit. Satisfied?

If you have good examples of math instruction that falls into one of these categories, or want to propose it, tweet or add it to the comments. I’m going to write up my own characterizations of this later. Hopefully not much later.

*******

Here’s what I originally said in the changed paragraph:

So Wiggins and Jay McTighe wrote Understanding by Design, which describes their framework and approach to curriculum. It is, as I said, a bible of ed schools. I have a copy. It’s good, although you have to look past their irritating examples to figure that out. The book clearly states that there’s no one right answer, that arguing between direction instruction or constructivism creates a false dichotomy, but then there’s this table on the activities dominant in each approach. Cough. Okay, no one right answer, but a strong preference for facilitative/constructivist.